Глава 1. Пространство-время и космология

Предлагаемая читателю книга называется «Большое, малое и человеческий разум», и поэтому в полном соответствии с названием две ее первые главы посвящены самым большим и самым малым объектам в окружающей нас физической Вселенной, которую я с предельной схематичностью и простотой изобразил в виде «сферы» на рис. 1.1. Я не буду тратить время на чисто «ботанические» описания того, что и как происходит в разных частях Вселенной, а попробую обратить ваше внимание на анализ и понимание реальных законов, управляющих ее поведением. Основная причина, по которой я разделил физические законы на части, относящиеся к «большому» и «малому», заключается в том, что общие закономерности физических процессов в очень большом и очень малом масштабах представляются весьма различными. Центральной темой гл. 3, где речь идет о человеческом сознании, является именно это бросающееся в глаза различие между законами природы для разномасштабных явлений. Поскольку я буду говорить о физическом мире на языке описывающих его физических теорий, я просто обязан сказать хоть что-то и о другом мире — мире Платона, философском представлении мира идей, абсолютов и математических истин. Конечно, платоновский мир содержит и другие абсолютные понятия (такие как Добро и Красота), но я в данном случае буду говорить лишь о математических принципах и понятиях. Некоторым людям трудно представить себе существование этого мира вообще, и они предпочитают считать математические понятия просто какими-то идеализированными формами объектов нашего физического мира, и в этом случае, конечно, «математический мир» следует рассматривать всего лишь как порождение нашего физического мира (рис. 1.2).

Рис. 1.1.

Рис. 1.2.

Я лично полагаю (и, мне кажется, большинство математиков и физиков-теоретиков придерживаются примерно той же точки зрения), что математика имеет другие, более серьезные основания и представляет собой некую структуру, управляемую собственными вневременными законами. Поэтому, возможно, многие физики и математики предпочли бы считать физический мир порождением «вневременного» математического мира идей. Соответствующая картина (рис. 1.3) при всей ее простоте очень важна для рассматриваемых в этой книге проблем (в особенности это относится к материалу гл. 3).

Рис. 1.3.

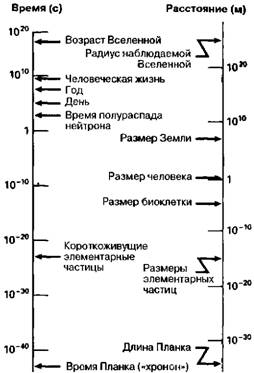
Наиболее замечательной характеристикой законов природы является то, что они подчиняются математическим закономерностям с исключительно высокой точностью. Чем глубже мы понимаем законы природы, тем сильнее чувствуем, что физический мир как-то исчезает, «испаряется», и мы остаемся лицом к лицу с чистой математикой, т. е. имеем дело лишь с миром математических правил и понятий.

Прежде чем перейти к дальнейшему рассмотрению, нам следует оценить временные и пространственные масштабы Вселенной и как-то связать их с местом и ролью человека в общей картине мира. Я сделал попытку объединить масштабы некоторых известных объектов и процессов в единую диаграмму (рис. 1.4), где слева представлены характерные времена, а справа — характерные размеры. В нижнем левом углу рисунка указан минимальный масштаб времени, имеющий какой-то физический смысл. Этот интервал времени, равный 10^-43 с, называется планковским временем, или «хрононом», и он намного короче продолжительности всех известных нам процессов, включая очень краткие процессы физики элементарных частиц (например, время существования самых короткоживущих частиц-резонансов составляет около 10^-23 с). Выше по диаграмме в логарифмическом масштабе указана длительность некоторых известных процессов, вплоть до возраста Вселенной.

Рис. 1.4. Характерное время и размеры некоторых объектов и процессов Вселенной.

Справа на диаграмме приведены расстояния, соответствующие определенным временным масштабам. Времени Планка (хронону) соответствует фундаментальная единица, называемая планковской длиной. Две эти величины естественным образом возникают при любой попытке объединить физические теории, описывающие очень большие и очень малые объекты (речь идет об общей теории относительности Эйнштейна и квантовой механике). При любом сочетании вариантов этих теорий длина и время Планка выступают в качестве фундаментальных единиц измерения. Переход от левой шкалы диаграммы к правой осуществляется умножением на скорость света, что позволяет легко сопоставлять любой промежуток времени с расстоянием, проходимым световым сигналом за это время.

Размеры физических объектов на рисунке изменяются от 10^-15 м (характерный размер элементарных частиц) до 10²⁷ м (радиус наблюдаемой Вселенной, приблизительно соответствующий ее возрасту, умноженному на скорость света). Интересно оценить положение, которое на диаграмме занимаем мы, люди.

На шкале размеров мы находимся где-то в середине, будучи чрезвычайно крупными по отношению к длине Планка (и превышая на много порядков размеры элементарных частиц), но очень маленькими в масштабах всей Вселенной. С другой стороны, на временной шкале процессов длительность человеческой жизни выглядит совсем неплохо, и ее можно сопоставлять с возрастом Вселенной! Люди (и в особенности поэты) любят жаловаться на эфемерность человеческого существования, однако наше место на временной шкале вовсе не является жалким или ничтожным. Разумеется, нам следует помнить, что все сказанное относится к «логарифмической шкале», однако ее использование представляется совершенно оправданным при рассмотрении столь гигантских диапазонов значений. Говоря другими словами, число человеческих жизней, укладывающихся в возрасте Вселенной, намного меньше, чем число времен Планка (или даже времен жизни элементарных частиц), укладывающихся в продолжительность жизни человека. В сущности, мы являемся довольно стабильными структурами Вселенной. Что же касается пространственных масштабов, то мы действительно находимся где-то в середине шкалы, вследствие чего нам не дано воспринимать в непосредственных ощущениях ни очень большие, ни очень малые объекты окружающего нас физического мира.

Давайте рассмотрим, какие физические теории описывают объекты столь различных размеров. В схему рис. 1.5 я попытался «втиснуть» всю существующую физику. При этом мне, конечно, пришлось пожертвовать многими незначительными деталями (например, просто выкинуть из картины все уравнения и разделы наук!), однако, на мой взгляд, я сохранил фундаментальные теории.

Рис. 1.5.

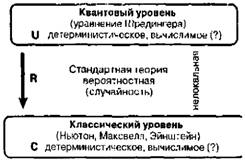
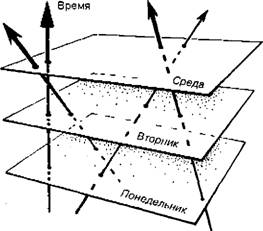
Наиболее существенным обстоятельством является то, что в физике используются два совершенно разных подхода. Для описания поведения микрообъектов мы используем квантовую механику (я обозначил ее на рисунке словами «квантовый уровень»), о которой подробнее рассказано в гл. 2. Большинство людей полагают, что квантовая механика является странной, загадочной и недетерминистической теорией, но это неверно. На самом деле, если вы рассматриваете события на квантовом уровне, то квантовая теория является совершенно точной и детерминистической. Наиболее известным ее соотношением является уравнение Шредингера, которое определяет поведение физического состояния квантовой системы (его называют просто квантовым состоянием) и, безусловно, является совершенно точным и детерминистическим. Я использую букву U для обозначения всех расчетов или методов, связанных с квантовым уровнем рассмотрения. Неопределенность в квантовой механике возникает лишь тогда, когда вы осуществляете так называемое «измерение», требующее значительного «увеличения» масштаба события для перехода с квантового уровня на классический. Более подробно мы будем рассматривать эти проблемы в гл. 2.

При больших масштабах мы используем представления классической физики, которая является совершенно детерминистической. Она включает в себя законы механики Ньютона, законы Максвелла (позволяющие ввести в физику понятия электричества, магнетизма и света), две теории относительности Эйнштейна (специальную теорию относительности, описывающую движение тел при больших скоростях, и общую теорию относительности для систем с мощными гравитационными полями), причем все эти законы выполняются при больших расстояниях с исключительно высокой точностью.

Отмечу также, что на рис. 1.5 я использовал термин «вычислимость» для характеристики и квантовой, и классической физики. В первых двух главах это понятие практически не используется, но оно имеет важное значение для задач, обсуждаемых в гл. 3, где мы и рассмотрим проблему «вычислимости» более внимательно.

Настоящая глава посвящена в основном эйнштейновской теории относительности, ее характерным особенностям, исключительной точности, а также поразительной изящности и элегантности. Однако сначала необходимо рассказать хотя бы очень кратко о ньютоновской физике. Вскоре после того, как Эйнштейн разработал общую теорию относительности, Картан показал, что ньютоновская теория гравитации также позволяет ввести представление о едином пространстве-времени. Физическая картина в механике Галилея и Ньютона позволяет представить пространство-время введением глобальной (всемирной) временной координаты, после чего состояние системы может описываться просто набором последовательных диаграмм (рис. 1.6), в которых различным моментам времени соответствуют сечения четырехмерного пространства-времени. Каждому такому пространственному сечению (т. е. плоскости на рис. 1.6) соответствует обычное евклидово трехмерное пространство. Характерной особенностью ньютоновского пространства-времени является то, что все пространственные «сечения» существуют в нем как бы одновременно.

Рис. 1.6. Единое пространство-время в механике Галилея—Ньютона. Прямые линии соответствуют равномерно движущимся частицам.

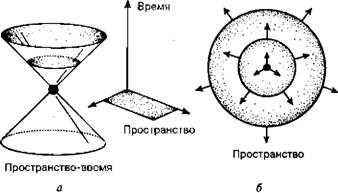
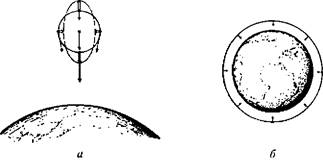
Таким образом, например, все события, происходящие в полночь понедельника, лежат в нижней горизонтальной плоскости диаграммы; все, что происходит в полночь вторника, — на следующей плоскости и т. д. Временные сечения по оси времени дают просто последовательность евклидовых пространств во времени. Все наблюдатели (независимо от их способа передвижения в пространстве-времени) фиксируют одни и те же события одновременно, поскольку они видят одни и те же «срезы», или «сечения», единого пространства-времени.

Совершенно иначе обстоят дела в специальной теории относительности Эйнштейна, где время и, соответственно, полная картина пространства-времени перестают быть универсальными величинами, как в физике Ньютона. Для демонстрации существенной разницы этих теорий нам необходимо прежде всего ввести одно из важнейших представлений теории относительности — так называемый световой конус.

Что такое световой конус? Представьте себе вспышку света в заданной точке пространства и в определенный момент времени (это и есть событие в пространстве-времени), после которой волны начинают распространяться со скоростью света, передавая сигнал о событии. В пространственных координатах фронт распространения имеет вид сферы, расширяющейся со скоростью света (рис. 1.7, б), однако в полной системе координат (пространство-время) мы получим значительно более сложную картину (рис. 1.7, а), в которой будут учитываться горизонтальные смещения, соответствующие сдвигам на рис. 1.6. К сожалению, изображение на рис. 1.7, а является всего лишь двумерным (плоскость рисунка), поскольку мы пользуемся всего лишь тремя измерениями для изображения четырехмерного пространства-времени. Поэтому нам приходится изображать вспышку света точкой в начале координат (событие), а затем — окружностями на горизонтальных сечениях, отражающими реальное движение лучей света (волн) через пространство. При этом движение световых лучей образует в пространстве-времени конус, верхняя часть которого описывает историю «вспышки» движением световых лучей в будущее пространство-время. С другой стороны, нижняя часть конуса соответствует приходу световых лучей из прошлого в точку вспышки (эту часть диаграммы обычно называют световым конусом прошлого). Наблюдатель получает всю информацию от световых лучей, распространяющихся по поверхности конуса!

Рис. 1.7. Распространение световой вспышки в пространстве-времени (а) и пространстве (б).

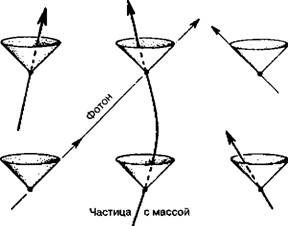
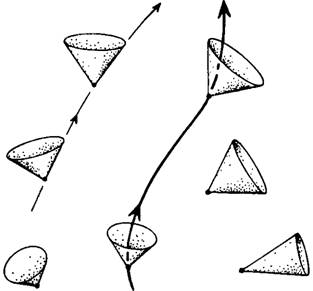
Такие световые конусы являются важнейшими структурами пространства-времени, и, в частности, именно они ограничивают возможности и пределы причинно-следственных связей в природе. Историю любой частицы можно изобразить линией в пространстве-времени на диаграмме указанного типа, причем эта линия должна лежать внутри светового конуса (рис. 1.8). Все сказанное просто вытекает из условия, что никакая материальная частица не может двигаться быстрее света. Поэтому никакой сигнал не может выйти за пределы светового конуса, что естественным образом ограничивает пределы действия любых причинно-следственных связей.

Рис. 1.8. Описание движения частицы в пространстве-времени специальной теории относительности

(его называют также пространством-временем Минковского или просто геометрией Минковского). Световые конусы в различных точках пространства-времени выстраиваются таким образом, что частицы могут двигаться лишь внутри световых конусов, относящихся к будущему.

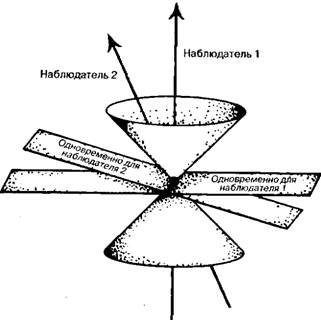
Естественно, что световые конусы отличаются весьма своеобразными геометрическими свойствами. Представим себе, например, двух наблюдателей, движущихся в пространстве-времени с различной скоростью. В отличие от механики Ньютона, где «плоскости одновременных событий» совершенно одинаковы для всех наблюдателей, в теории относительности нельзя ввести абсолютную одновременность, вследствие чего каждый из этих наблюдателей будет рисовать собственные плоскости «одновременности» в пространстве-времени, как показано на рис. 1.9. Существует известный и хорошо разработанный метод преобразования таких плоскостей друг в друга (так называемые преобразования Лоренца, образующие группу Лоренца), открытие которого сыграло важную роль в истории специальной теории относительности. Речь идет о группе (линейных) преобразований пространства-времени, при которых световой конус остается инвариантным.

Рис. 1.9. Относительность понятия одновременности в специальной теории относительности Эйнштейна.

Наблюдатели 1 и 2 движутся в пространстве-времени относительно друг друга, в результате чего события, одновременные для наблюдателя 1, перестают быть одновременными для наблюдателя 2, и наоборот.

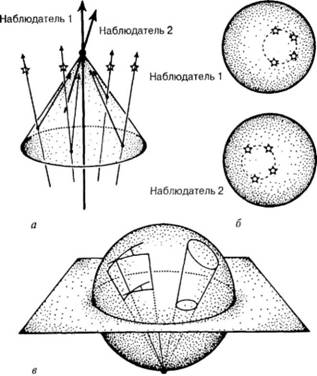
Мы можем придать группе Лоренца и несколько иную трактовку. Как уже подчеркивалось, световой конус является одной из важнейших структур пространства-времени. Представьте себя наблюдателем, рассматривающим Вселенную из какой-то точки пространства. В ваши глаза попадает свет от далеких звезд, и в соответствии с концепцией пространства-времени наблюдаемые вами события представляют собой пересечения мировых линий звезд с вашим световым конусом прошлого, как это показано на рис. 1.10. Другими словами, в вашем световом конусе прошлого звезды в некоторый момент времени образуют некий рисунок на небесной сфере (рис. 1.10, а). Предположим, что второй наблюдатель, двигаясь с большой скоростью относительно вас, именно в этот момент оказывается рядом. Он воспринимает те же звезды, однако ему кажется, что они занимают на сфере другие положения (рис. 1.10, б) — этот эффект астрономы называют аберрацией. Существует набор преобразований, позволяющий связать друг с другом изображения, воспринимаемые различными наблюдателями. В каждом из таких преобразований сфера соотносится с другой сферой, однако среди этих преобразований есть специальное, в котором точным окружностям соответствуют точные окружности, в результате чего при преобразовании сохраняются значения углов, т. е. воспринимаемые вами круглые изображения остаются круглыми и для другого наблюдателя.

Рис. 1.10. Картина звездного неба для двух различных наблюдателей,

а — наблюдатели 1 и 2 из одной и той же точки рассматривают звезды в световом конусе прошлого. Места пересечения светового конуса со звездами указаны черными точками. Световые сигналы идут от звезд к наблюдателям вдоль светового конуса. Наблюдатель 2 движется в пространстве-времени относительно наблюдателя 1 с некоторой скоростью; б — расположение звезд на небе, как его видят наблюдатели 1 и 2, когда они оказываются в одной точке пространства-времени; в — наглядное представление преобразования картины звездного неба для различных наблюдателей при использовании стереографической проекции (окружности переходят в окружности, значения углов сохраняются).

Существует прекрасная иллюстрация механизма действия таких преобразований, которая, кстати, одновременно демонстрирует исключительную элегантность и красоту математической физики при описании фундаментальных понятий и представлений. На рис. 1.10, в показана сфера, пересекаемая плоскостью по экватору. Мы можем нарисовать на поверхности этой сферы различные фигуры, а затем рассмотреть их так называемые стереографические проекции (проекции из южного полюса сферы на экваториальную плоскость), обладающие довольно необычными свойствами. Действительно, как видно из рисунка, при такой проекции не только окружности на сфере превращаются в окружности на плоскости, но сохраняются и точные значения всех углов, образуемых пересечением кривых на сфере. В гл. 2 я более подробно расскажу об этом типе проекций (см. рис. 2.4) и покажу, что с его помощью можно сопоставить все точки сферы комплексным числам (такие числа возникают при извлечении квадратного корня из отрицательных чисел), а затем перевести в точки экваториальной плоскости. Такая операция, в которую можно вовлечь все множество комплексных чисел (включая «бесконечные» значения), позволяет построить структуру, называемую сферой Римана.

Для читателя, заинтересовавшегося этой проблемой, я приведу формулу

u -> u' = (?u + ?) / (?u + ?),

описывающую преобразование (аберрации) Лоренца, которое переводит окружности в окружности и одновременно сохраняет значения всех углов. Преобразования такого типа называют преобразованиями Мёбиуса. Мне бы хотелось лишь отметить простоту и изящество этой формулы, описывающей столь сложный параметр, каким выступает в данной ситуации величина и. Совершенно удивительным кажется то, что при указанных преобразованиях в специальной теории относительности конечная формула имеет очень простой вид, в то время как соответствующие преобразования аберрации в ньютоновской механике описываются очень сложными выражениями. Как это часто бывает в физике, переход к более фундаментальным понятиям и более точным теориям приводит к упрощению математического описания, хотя на первый взгляд такой переход должен сопровождаться усложнением формального аппарата. Примером этой важной закономерности может служить разительный контраст между понятиями относительности в механике Галилея и Эйнштейна.

Специальная теория относительности во многих отношениях не только значительно проще классической механики, но и выглядит гораздо изящнее с математической точки зрения (в частности, при рассмотрении процессов в рамках теории групп). В специальной теории относительности пространство-время является плоским, а все световые конусы выстраиваются вдоль траекторий, как было показано на рис. 1.8. При переходе к более сложной общей теории относительности (теории пространства-времени с учетом гравитации) ясная физическая картина на первый взгляд «мутнеет» и теряет свою простоту, так как световые конусы оказываются разбросанными по всему пространству (рис. 1.11). Ранее я говорил, что, развивая любую теорию все глубже и глубже, мы должны приходить к более простым математическим выражениям. Представленная мною картина пока выглядит ужасающе сложной, однако если мы проявим немного терпения, то убедимся, что математическая простота и изящество теории возникнут снова.

Рис. 1.11. Искривленное пространство-время.

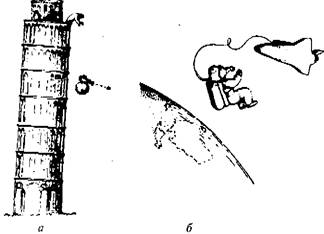
Напомню вам основные положения эйнштейновской теории тяготения. Прежде всего, она основана на принципе эквивалентности Галилея. На рис. 1.12 я попытался изобразить Галилея, бросающего с вершины знаменитой Пизанской башни большой и маленький камни. Независимо от того, действительно ли Галилей проводил такие эксперименты, он совершенно ясно установил, понял и сформулировал правило, что оба камня долетят до поверхности Земли за одинаковое время, если не учитывать сопротивления воздуха при падении. Если бы вы находились на одном из этих камней, то второй казался бы вам неподвижно висящим в воздухе (для более наглядной демонстрации этого факта я пририсовал телекамеру к одному из камней). В наше время эффект свободного парения очень часто демонстрируют при репортажах с космических кораблей, и недавно я сам видел британского космонавта, свободно «плавающего» в пространстве рядом с огромным космическим аппаратом (полная аналогия с большим и маленьким камнями в опытах Галилея). Именно это явление и называют принципом эквивалентности.

Рис. 1.12.

а — Галилей бросает с наклонной Пизанской башни два камня (один с телекамерой); б — астронавт и космический корабль, плавающие в пространстве как бы без воздействия гравитации.

Рассматривая гравитацию в рамках опытов со свободным падением, мы вдруг понимаем, что в этих условиях она как бы полностью исчезает. Однако эйнштейновская теория вовсе не утверждает, что тяготение исчезает, она всего лишь говорит об исчезновении силы тяжести, что означает совершенно иное явление, которое можно назвать «приливным эффектом» гравитации.

Для дальнейшего изложения мне необходимо ввести еще несколько математических понятий. Мы говорим об искривлении пространства-времени, а процессы такого типа описываются тензором, который я для удобства назову Риманом и буду обозначать заглавной буквой R в простом уравнении, которое выпишу чуть ниже. Я не буду объяснять вам, в чем состоит физический смысл тензора кривизны Римана, обозначенного R, а только отмечу, что тензоры имеют некоторое число нижних индексов, вместо которых в уравнение поставлено соответствующее число точек (внизу справа от знака тензора). Тензор кривизны R можно разложить на две составляющие (одну из которых я назову кривизной Вейля, а вторую — кривизной Риччи), что позволяет мне выписать уравнение

Риман = Вейль + Риччи

R.... = C... +R'...g..,

где формально величины С и R' являются тензорами кривизны Вейля и Риччи, a g — так называемый метрический тензор.

Кривизна Вейля является объективным показателем упомянутого выше «приливного эффекта», физическую природу которого я поясню сейчас на простом примере. С точки зрения космонавта гравитация исчезает, однако мы понимаем, что это не так. Представьте себе, например, что космонавт окружен сферическим облаком неподвижных относительно него частиц. С течением времени это облако начнет «расплываться» и деформироваться, после чего в результате очень небольшого различия сил тяготения в различных участках сферы (мне хочется особо подчеркнуть, что я могу вполне адекватно описать эффект в рамках ньютоновской механики) сферическое облако через некоторое время превратится в эллипсоид, как показано на рис. 1.13, а.

Рис. 1.13.

а — приливный эффект. Широкие стрелки показывают направление относительного ускорения частиц; б — если сферическое облако окружает какой-либо массивный объект (например, Землю), то оно испытывает в целом ускорение, направленное «внутрь».

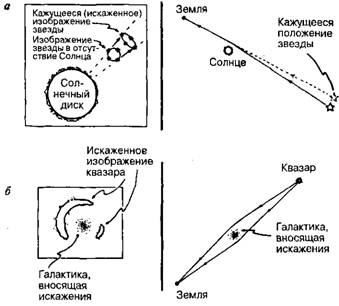
Как я уже говорил, искажение отчасти объясняется тем, что частицы, расположенные ближе к Земле, ускоряются сильнее, чем частицы на периферии облака. Кроме того, частицы по «бокам» сферы испытывают небольшие ускорения «внутрь», что также показано на рис. 1.13, а. Обе эти причины способствуют образованию эллипсоида из первоначально сферического облака частиц. Описываемый эффект очень удачно был назван «приливным», поскольку достаточно заменить Землю в наших рассуждениях Луной, а облако частиц — мировым океаном, как мы сразу поймем, почему поверхность морей на нашей планете не представляет собой правильную сферу! В соответствии с совершенно таким же механизмом морская толща на обращенной к Луне поверхности Земли притягивается Луной чуть сильнее, чем на обратной стороне, в результате чего вдоль морской поверхности дважды в день пробегает высокая приливная водна.

Гравитационный эффект по Эйнштейну представляет собой просто другую форму описанного приливного эффекта. Он определяется, как уже отмечалось, кривизной Вейля, т. е. составляющей С... выписанного выше уравнения. Эта часть тензора кривизны соответствует процессам с «сохранением объема» (т. е. объем эллипсоида, образовавшегося в результате деформации сферы из частиц, должен в точности равняться объему исходной сферы).

Вторая составляющая, называемая кривизной Риччи, относится к эффектам, связанным с «сокращением объема». Например, если Земля будет окружена сферическим облаком частиц (как показано на рис. 1.13, б), то объем сферы с течением времени должен несколько уменьшиться, поскольку все частицы притягиваются «внутрь». Степень такого сокращения объема и описывается составляющей R'. В соответствии с эйнштейновской теорией эта кривизна определяется количеством вещества в ближайшем окружении данной точки. Иными словами, определив правильным образом плотность вещества в некоторой точке пространства, мы можем найти и величину направленного «внутрь» ускорения. При таком подходе теория Эйнштейна полностью совпадает с ньютоновской теорией тяготения.

Именно так Эйнштейн и сформулировал свою теорию гравитации — он выразил тяготение посредством приливных эффектов, являющихся мерой локального искривления пространства-времени. Представление об искривлении четырехмерного пространства-времени является важнейшим в теории относительности. Я напомню вам рис. 1.11, где схематически были показаны мировые линии частиц и их искажения. Теория Эйнштейна представляет собой чисто геометрическую схему для четырехмерного пространства-времени, причем ее математическая формулировка отличается удивительной красотой.

История открытия общей теории относительности является весьма поучительной и интересной. Эйнштейн полностью сформулировал ее в 1915 г., исходя не из экспериментальных наблюдений, а лишь из некоторых эстетических, геометрических и физических принципов и пристрастий. Основой теории стали принцип эквивалентности Галилея (примером действия которого могут служить описанные выше эксперименты с бросанием камней различного веса, рис. 1.12) и общие идеи неевклидовой геометрии, естественным образом используемые для описания пространства-времени. Об экспериментальных доказательствах теории вначале никто не задумывался, однако после ее окончательной формулировки было предложено три разных варианта проверки. Первый из них связан с известной астрономической задачей (проблема смещения перигелия Меркурия), которую никак не удавалось решить в рамках классической механики Ньютона. Общая теория относительности позволила совершенно точно предсказать величину этого смещения. Далее, из теории следовало, что траектория световых лучей должна искривляться при прохождении через мощные гравитационные поля (например, вблизи Солнца). Для проверки этой гипотезы в 1919 г. под руководством Артура Эддингтона была организована астрономическая экспедиция для наблюдения полного солнечного затмения. Результаты, полученные этой знаменитой экспедицией, соответствовали предсказаниям эйнштейновской теории (рис. 1.14, а). И наконец, третья проверка была связана с предсказанием замедления хода часов в гравитационном поле (часы у поверхности Земли должны идти чуть медленнее, чем часы на вершине башни), что неоднократно проверялось в экспериментах. Следует отметить, что все эти проверки не оказались достаточно вескими (из-за того, что наблюдаемые эффекты всегда очень слабы), а также могут быть достаточно убедительно объяснены в рамках других теорий.

Рис. 1.14.

а — прямые измерения воздействия гравитационного поля на прохождение световых лучей в соответствии с общей теорией относительности. Изображение удаленных звезд искажается из-за вейлевского искривления пространства-времени, приводящего к искривлению траекторий световых лучей в гравитационном поле Солнца. Круглые изображения звезд при этом превращаются в эллипсы; б — использование эйнштейновского эффекта искривления световых лучей в качестве практического приема астрономических наблюдений. Массу галактики, лежащей на пути светового луча, можно оценить по степени искажения изображения удаленного квазара.

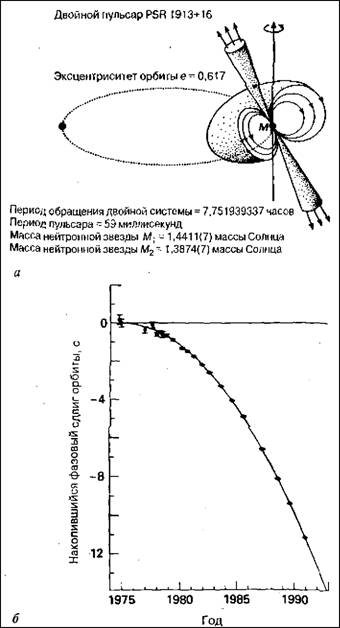
Отношение к теории относительности резко изменилось в 1993 г., когда Хульзе и Тейлор получили Нобелевскую премию за исключительно интересные астрономические наблюдения, относящиеся к двойному пульсару PSR 1913+16. Этот астрономический объект (рис. 1.15, а) состоит из двух нейтронных звезд со столь большой плотностью, что масса каждой из них примерно равна массе нашего Солнца, хотя их радиус составляет всего лишь несколько километров! Нейтронные звезды вращаются вокруг общего центра тяжести по очень вытянутым эллиптическим орбитам. Одна из звезд обладает сильнейшим магнитным полем, благодаря чему является источником настолько интенсивного излучения, что на Земле (т. е. на расстоянии 30 000 световых лет) оно прекрасно регистрируется в виде серии четко определенных импульсов. Это позволило провести разнообразные и тщательные измерения, в частности, параметры орбит обеих нейтронных звезд удалось замерить с очень высокой точностью и проверить поправки, связанные с учетом общей теории относительности.

Рис. 1.15.

а — схематическое изображение двойного пульсара PSR 1913+16. Одна из нейтронных звезд является источником направленного радиоизлучения, испускаемого вдоль оси магнитного диполя (которая, кстати, не совпадает с осью вращения нейтронной звезды). Отчетливые импульсы регистрируются в те моменты времени, когда узкий луч излучения попадает в поле зрения наблюдателя. Характеристики двойной нейтронной звезды, определяемые точной регистрацией сигналов, совпадают с теми, которые предсказывает общая теория относительности; б — сравнение экспериментально измеренных значений изменения фазы сигналов излучения пульсара PSR 1913+16 с теоретическими расчетами, основанными на учете гравитационного излучения двойной нейтронной звезды (сплошная кривая).

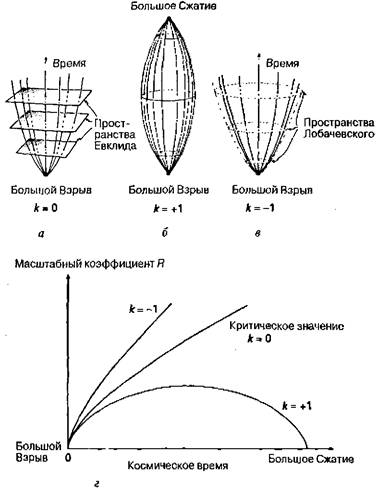
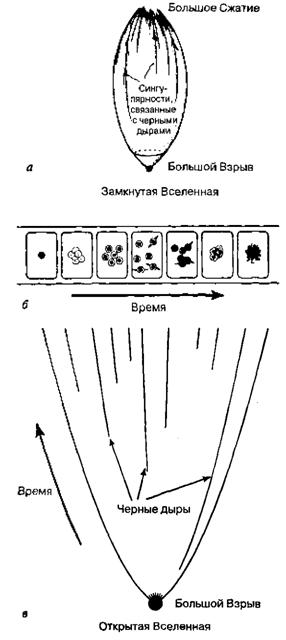
Далее я должен особо подчеркнуть, что в общей теории относительности существует и совершенно специфический эффект, отсутствующий в ньютоновской теории тяготения и заключающийся в том, что вращающиеся относительно друг друга объекты излучают энергию в виде гравитационных волн. Эти волны похожи на световые, но в отличие от последних представляют собой не колебания электромагнитного поля, а возмущения, или «рябь», пространства-времени. Измеренная скорость потери энергии упомянутой двойной нейтронной звезды с высокой точностью совпала с теоретическими расчетами, проведенными в рамках общей теории относительности. На рис. 1.15, б представлены результаты измерения смещения орбит за 20-летний период наблюдений. Высокая надежность регистрации излучаемых сигналов и длительность измерений позволили довести точность расчета параметров орбит до10^-14, что делает общую теорию относительности самой точной и проверяемой областью современной науки.

Процесс создания и проверки общей теорией относительности содержит, безусловно, и важный моральный мотив, связанный с тем, что Эйнштейн потратил на создание теории многие годы, практически не обращая внимания на проблемы ее экспериментальной проверки. Существует общераспространенное мнение, что физики ищут образы, или «паттерны», получаемых в эксперименте результатов и ставят своей целью создание красивых теорий, позволяющих описать эти результаты. Считается, что именно поэтому физики и математики предпочитают «держаться вместе». Однако в случае с общей теорией относительности ситуация выглядит совершенно иной. Вне всякой связи с экспериментальными результатами была разработана весьма изящная и элегантная математическая теория, относящаяся к основам физики. Проблема заключается как раз в том, что эта прекрасная математическая структура просто существует в Природе и присутствует в пространстве, а не является чем-то привнесенным, «навязанным» Природе извне. Одна из важнейших идей этой главы состоит в том, что Эйнштейн выявил в мире нечто, уже содержавшееся в нем. При этом обнаруженные им структуры вовсе не относятся к незначительным или маловажным разделам физики, а связаны с наиболее фундаментальными законами Природы и свойствами пространства-времени.

Сказанное возвращает нас к началу книги и рис. 1.3, связывающему мир математики с миром физических явлений. В общей теории относительности мы сталкиваемся со структурой, которая реально определяет с исключительной точностью поведение физического мира. При этом теория, описывающая фундаментальные свойства нашего мира, была получена вовсе не в результате длительных наблюдений за поведением Природы (разумеется, сказанное не означает, что я отрицаю очевидную ценность таких наблюдений). Конечно, основным критерием научной теории является не убедительность доводов, а соответствие фактам. В данном случае мы имеем дело именно с теорией, которая прекрасно согласуется с экспериментальными данными. Точность теории относительности по крайней мере вдвое (как математик я подразумеваю под точностью число знаков после запятой при надежном расчете) выше точности классической механики, т.е. ее расчеты справедливы до 10^-14 , в то время как точность ньютоновской механики составляет лишь 10^-7. Такое «возрастание» точности наблюдалось в классической механике за период от семнадцатого века (Ньютон знал, что точность его расчетов составляет 10^-3) до наших дней (она доведена, как я уже говорил, до10^-7).

Разумеется, гипотеза Эйнштейна представляет собой некую физическую теорию, и для нас очень важно установить ее связь со структурой реального мира. Я обещал, что не буду вдаваться в подробности и делать изложение «ботаническим», однако в данном случае речь идет о теории единственной известной нам Вселенной (как о целостном объекте), так что я могу углубиться в рассуждения, не опасаясь обвинений в излишней болтливости. Теория Эйнштейна предлагает нам три типа стандартной модели развития мира (рис. 1.16) в зависимости от того, какова величина одного из главных параметров теории, обозначенного буквой k. В различных работах по космологии часто используется так называемая космологическая постоянная, но я не буду ее упоминать, поскольку сам Эйнштейн считал своей основной ошибкой именно введение этой постоянной в уравнения общей теории относительности. Если же жизнь когда-нибудь заставит физиков вернуться к этой постоянной, нам придется это вытерпеть.

Рис. 1.16.

а — пространственно-временная картина расширяющейся Вселенной с евклидовыми пространственными сечениями (на рисунке указаны лишь два измерения), k = 0; б — пространственно-временная картина расширяющейся (а затем сжимающейся) Вселенной со сферическими пространственными сечениями, k = +1; в — пространственно-временная картина расширяющейся Вселенной с пространственными сечениями, описываемыми геометрией Лобачевского, k = -1; г — динамика развития трех указанных типов модели Фридмана.

Полагая космологическую постоянную равной нулю, мы получаем для трех различных значений параметра k (k = +1, 0, -1) три различные модели Вселенной (см. рис. 1.16). Разумеется, было бы правильнее учитывать также возраст и масштаб Вселенной (для этого необходимо пользоваться непрерывным, а не дискретным параметром k), однако мы ограничимся лишь этими тремя моделями, поскольку их можно легко связать с кривизной пространственных сечений Вселенной. Если сечения являются плоскими, то этому соответствует нулевая кривизна и значение параметра k = 0 (рис. 1.16, а). Если же сечения имеют положительную кривизну, то Вселенная является замкнутой и, следовательно, k = +1 (рис. 1.16, б). В этих моделях Вселенная имеет сингулярное исходное состояние, знаменующее ее рождение (знаменитый Большой Взрыв). При k = +1 Вселенная после рождения расширяется (иногда говорят «раздувается») до некоторого максимального размера, после чего начинает сжиматься и «схлопывается» в момент Большого Сжатия. При k = -1 расширение Вселенной будет продолжаться вечно (рис. 1.16, в), а случай k = 0 является промежуточным между двумя указанными. На рис. 1.16, г схематически показана зависимость радиуса Вселенной от времени, где под радиусом понимается некий характерный размер. Он может быть задан лишь при k = +1, а в двух остальных случаях Вселенная просто бесконечно расширяется.

Мне хочется подробнее рассмотреть случай с k = -1 (который, кстати сказать, труднее всего согласовать с общей картиной), представляющий интерес по двум важным причинам. Во-первых, эта модель наиболее удобна, если вы хотите трактовать результаты наблюдений по их истинному, «номинальному» значению. Дело в том, что в общей теории относительности искривление пространства обусловлено суммарным количеством вещества во Вселенной, а этого количества, по современным данным, явно недостаточно для создания Вселенной с замкнутой геометрией (разумеется, может оказаться и так, что Вселенная содержит большое количество так называемой скрытой, или темной, массы, которую мы еще просто не успели обнаружить, и тогда будет справедлива какая-то другая модель, однако, скорее всего, наша Вселенная не имеет столь большой массы и описывается параметром k = -1). Вторая причина моего интереса к этой модели связана с ее исключительной красотой и элегантностью.

На что похожи вселенные с параметром k = -1? Их пространственные сечения описываются так называемой гиперболической геометрией (геометрией Лобачевского), прекрасной иллюстрацией которой может служить одна из картин Мориса Эшера (рис. 1.17). Эшер нарисовал целую серию гравюр, озаглавленную «Предельные окружности», одна из которых и показана на рисунке. Как вы видите, художнику представляется, что Вселенная полна ангелов и чертей! Для нашего рассмотрения гораздо важнее то, что вся картина как бы выгнута по отношению к краям предельной окружности, и это искривление связано именно с попыткой художника изобразить гиперболическое пространство на плоском листе бумаги, иными словами — в привычном евклидовом пространстве. Следует осознать, что если бы мы жили в этой Вселенной, то форма и размеры всех чертей были бы одинаковы независимо от того, попали бы мы в центр или на край картины. Гравюра дает некоторое представление о том, что происходит в пространстве Лобачевского, и о тех особенностях, которые возникают при соответствующем искажении пространства.

Рис. 1.17. М. Эшер. «Предельная окружность 4» (представление геометрии Лобачевского).

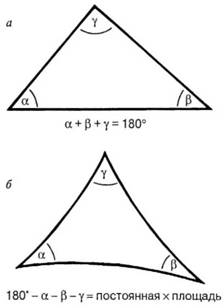
Геометрия Лобачевского может показаться странной и неожиданной, но если вдуматься, то привычная нам евклидова геометрия — тоже совершенно замечательная вещь, хотя бы потому, что она дает нам прекрасные образцы взаимодействия физики и математики. Когда-то древние греки рассматривали ее не как раздел математики, а как описание окружающего мира.

Геометрия действительно описывает мир с поразительной точностью. Я говорю об очень высокой, но не абсолютной точности, поскольку, как мы уже видели, теория Эйнштейна доказала позднее, что наш мир в определенных условиях может быть «искривлен». Вопрос о возможности существования других геометрий всегда волновал ученых. Эта очень старая проблема известна под названием пятого постулата Евклида и сводится к справедливости утверждения о том, что через точку на плоскости, лежащую вне заданной прямой, можно провести только одну прямую, параллельную данной. Долгое время считалось, что это утверждение можно доказать, используя другие, более очевидные теоремы и положения евклидовой геометрии, однако позднее выяснилось, что такое доказательство невозможно, вследствие чего и возникло представление о неевклидовой геометрии.

В такой геометрии сумма углов треугольника не равна 180°. На первый взгляд кажется, что это условие значительно усложняет рассмотрение, поскольку мы привыкли к тому, что в евклидовой геометрии сумма углов любого треугольника всегда составляет именно 180° (рис. 1.18, а). Однако в неевклидовой геометрии разность между суммой углов треугольника и 180° пропорциональна площади треугольника, т. е. неожиданно выясняется, что площадь треугольника сложнее описать именно в евклидовой геометрии, где она задается сложным уравнением для всех углов и длин сторон треугольника. В неевклидовой геометрии площадь треугольника определяется замечательно простой формулой Ламберта (рис. 1.18, б). Поразительно, но Ламберт вывел свою формулу до открытия неевклидовой геометрии!

Рис. 1.18.

а — треугольник в евклидовом пространстве; б — треугольник в пространстве Лобачевского.

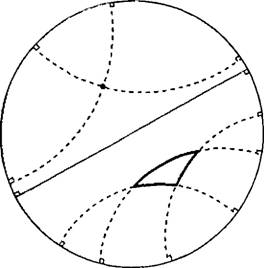
Очень важную роль в геометрии играют так называемые действительные (вещественные) числа, абсолютно необходимые для построений евклидовой геометрии. Такие числа ввел древнегреческий математик Евдокс в 4 веке до н.э., и они до сих пор сохраняют свое значение для создания физической картины мира. Позднее мы будем говорить и о комплексных числах, но последние также основаны на представлении о вещественных числах.

Давайте рассмотрим еще одну гравюру Эшера (рис. 1.19), которая демонстрирует особенности геометрии Лобачевского даже нагляднее, чем рис. 1.17 (поскольку на ней использованы «прямые линии», которые всегда выглядят более очевидными). На рисунке показаны дуги окружностей, пересекающие границу под прямым углом. Обитатель мира с геометрией Лобачевского воспринимал бы прямую линию как одну из этих дуг, что хорошо видно на рис. 1.19, где «по-настоящему прямыми» являются лишь линии, проходящие через центр окружности, а все остальные «прямые» в действительности представляют собой изогнутые дуги. Некоторые из этих «прямых» показаны на рис. 1.20, где я дополнительно выделил точку, не лежащую на истинной прямой (т. е. не на диаметре). Обитатель мира Лобачевского может провести через эту точку две (и даже больше) различные линии, которые не будут пересекать диаметр, т. е. в этой геометрии пятый постулат Евклида безусловно не имеет силы. Более того, измерив сумму углов треугольника на рисунке, вы можете вычислить его площадь. Надеюсь, что даже эти обрывочные сведения дают возможность почувствовать необычность и очарование мира с гиперболической геометрией.

Рис. 1.19. Гравюра М. К. Эшера «Предельная окружность 1».

Рис. 1.20. Некоторые особенности гиперболической геометрии (пространства Лобачевского), поясняющие построения гравюры «Предельная окружность 1».

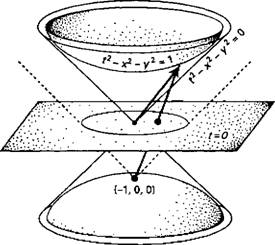
Я уже говорил, что мне очень нравится гиперболическая геометрия, созданная Лобачевским. Одной из причин моего пристрастия является и то, что группой симметрий этого пространства выступает уже знакомая нам группа Лоренца, соответствующая симметрии специальной теории относительности и световых конусов, играющих в этой теории столь важную роль. На рис. 1 .21 световой конус показан более подробно. Я нарочно убрал одну из пространственных координат, чтобы продемонстрировать вам наглядную трехмерную картину. Показанный на рисунке световой конус описывается простым уравнением

t² - x² - y² = 0.

Рис. 1.21. Пространство Лобачевского, «вложенное» (в виде гиперболоидов) в пространство-время Минковского.

Стереографическая проекция переводит его в так называемый диск Пуанкаре, ограниченный окружностью на плоскости t = 0.

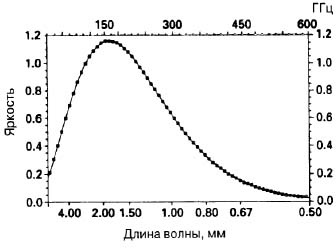
В такой геометрии (ее называют геометрией Минковского) уравнению t² - x² - y² = 0 соответствуют две чашеобразные поверхности, расположенные на «единичном расстоянии» от начала координат («расстоянию» в геометрии Минковского соответствует реальное время, т. е. время, измеряемое в физическом эксперименте при помощи движущихся часов). В пространстве Минковского эти поверхности служат «сферами», и можно показать, что внутренняя геометрия таких сфер является гиперболической (пространство Лобачевского). В евклидовой геометрии вы можете вращать обычную сферу и найти группу симметрии, соответствующую таким вращениям. В случае поверхностей, изображенных на рис. 1.21, группа симметрий представляет собой группу вращений Лоренца, которая описывает преобразование пространства и времени при вращении, т. е. при вращении единого пространства-времени вокруг некоторой фиксированной точки. В таком представлении группа симметрий пространства Лобачевского точно совпадает с группой Лоренца.

На рис. 1.21 для пространства Минковского показана также стереографическая проекция, подобная рассмотренной выше (рис. 1.10, в). Вместо южного полюса на рис. 1.21 используется точка (-1, 0, 0), а точки верхней «чаши» проецируются на плоскость t = 0, которая выступает аналогом экваториальной плоскости на рис. 1.10, в. Все точки после проецирования лежат внутри окружности в плоскости t = 0, которую называют иногда диском Пуанкаре. В результате операции в целом (которая, кстати, в точности совпадает с художественным приемом, использовавшимся М.Эшером в его гравюрах «Предельная окружность») гиперболическая поверхность (пространство Лобачевского) преобразуется в диск Пуанкаре. Более того, такое преобразование соответствует главной особенности проекции рис. 1.10, в — оно сохраняет все углы и окружности, придавая операции геометрическое изящество. Я просто восхищаюсь всеми этими совпадениями, с которыми математики постоянно встречаются в своих исследованиях!

Надеюсь, что мой восторг не показался вам чрезмерным. Существует интересная и несколько загадочная психологическая закономерность: если результаты исследования какой-то заинтересовавшей вас проблемы (например, геометрической) выражаются красивой математической формулой, то это поддерживает интерес исследователя и стимулирует дальнейшую работу (совершенно аналогично результаты, не обладающие математическим изяществом, обычно разочаровывают и обескураживают исследователя). Гиперболической геометрии присуща особая математическая красота, и было бы очень приятно (мне лично, по крайней мере), если бы Вселенная была построена столь математически красиво. Разумеется, у меня есть очень много других причин для веры в такое устройство Вселенной. Многим не нравится идея о гиперболической, открытой Вселенной, и они предпочитают модели замкнутых вселенных (типа показанных на рис. 1.16, б), которые, вполне возможно, кажутся им более приятными и уютными (разумеется, стоит отметить, что такие замкнутые вселенные все еще остаются весьма крупными). Другие ученые предпочитают модели плоского мира (рис. 1.16, а), поскольку среди теорий зарождения Вселенной существует и так называемая теория раздувающейся Вселенной, предполагающая плоскую геометрию мира. Должен сказать, что я не очень доверяю этим теориям.

Описанные выше три стандартных типа моделей Вселенной, известные под общим названием моделей Фридмана, отличаются исключительно высоким уровнем симметрии. Все они описывают расширение, однако Вселенная при этом остается совершенно однородной в любой момент времени. Это условие входит в структуру моделей Фридмана и получило специальное название космологического принципа. В моделях Фридмана свойства Вселенной одинаковы по всем направлениям, и похоже, что наша Вселенная устроена действительно по этому принципу. Если уравнения Эйнштейна справедливы (а выше я говорил о том, что его теория с высокой степенью точности соответствует наблюдаемым явлениям), то к моделям Фридмана следует относиться весьма серьезно. Отметим, что во всех этих моделях присутствует не очень «изящный» с точки зрения физики Большой Взрыв (состояние сверхгорячей Вселенной с бесконечной плотностью и другими сингулярными параметрами, которые очень трудно описывать теоретически). Однако если мы все же смиримся с возможностью существования этого сверхнагретого и сверхплотного физического состояния, то сможем предсказать развитие мира вплоть до настоящего времени. Одно из важнейших предсказаний такого типа относится к тепловому состоянию Вселенной. Теоретический расчет показывает, что в ней должно присутствовать однородное фоновое излучение, спектр которого должен соответствовать известному в физике излучению черного тела. Именно такой тип космической радиации (получивший название микроволнового фонового излучения) был открыт Пензиасом и Вильсоном в 1965 г., что стало одной из главнейших научных сенсаций нашего времени. На рис. 1.22 представлена спектральная кривая этого излучения (полученная при помощи спутника СОВЕ), которая с очень высокой степенью точности совпадает с хорошо известным из учебников спектром абсолютно черного тела.

Рис. 1.22. Результаты измерений спектра космического микроволнового фонового излучения

(точки на рисунке), полученные при помощи спутника СОВЕ, прекрасно совпадают с расчетной кривой (сплошная линия), полученной из «тепловой» теории Большого Взрыва.

Для всех специалистов по космологии существование этого фонового излучения стало убедительным доказательством того, что наша Вселенная когда-то находилась в очень горячем и плотном состоянии. Излучение сообщает нам нечто об исходном состоянии Вселенной и, хотя не дает полной информации, совершенно определенно свидетельствует о том, что событие типа Большого Взрыва действительно когда-то произошло.

Другими словами, наша Вселенная должна быть очень похожа на одну из моделей рис. 1.16.

Измерения, проведенные при помощи спутника СОВЕ, позволили сделать еще одно важное открытие, заключающееся в том, что (хотя обнаруженное космическое фоновое излучение является высокооднородным и прекрасно описывается математически) Вселенная в целом не является совершенно однородной. В распределении излучения по звездному небу остаются очень небольшие, но вполне реальные неоднородности. Фактически мы вынуждены признать, что какие-то крошечные неоднородности присутствовали уже на самой ранней стадии развития Вселенной, а сейчас мы видим лишь их остатки, которые еще не «расплылись» и не превратились в однородное «загрязнение». Скорее всего, наша Вселенная похожа на модели рис. 1.23 (для демонстрации своей непредубежденности и беспристрастности я привожу примеры и открытой, и замкнутой Вселенной).

Рис. 1.23.

a — модель эволюции замкнутого мира с образованием черных дыр в виде объектов разного типа, достигших конечного состояния в своем развитии. Легко сообразить, что в этом случае к моменту гибели мира (Большому Сжатию, или Коллапсу) будет твориться ужасное «столпотворение»; б — развертка событий рис. а в виде набора отдельных «фотокадров»; в — эволюция Вселенной открытого тина с образованием черных дыр на разных этапах развития.

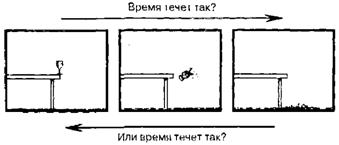
Развитие неоднородностей в замкнутой Вселенной будет приводить к образованию реальных наблюдаемых структур (звезд, галактик и т. д.), после чего в результате коллапса звезд, стягивания масс галактик к центрам и т. п. начнут формироваться черные дыры со своими сингулярными центрами (картина будет напоминать Большой Взрыв, протекающий в обратном порядке). Однако в целом ситуация не столь проста. Дело в том, что исходное состояние Большого Взрыва было приятно симметричным и однородным, а изображенное на рисунке конечное состояние представляет собой ужасную «смесь», в которой образующиеся черные дыры сбиваются в кучи, производя немыслимый беспорядок в момент Большого Сжатия (рис. 1.23, а). На рис. 1.23, б эволюция такой замкнутой модели представлена в виде последовательности «фотокадров», фиксирующих ряд событий. В модели открытой Вселенной образование черных дыр выглядит гораздо естественнее и «спокойнее» — во Вселенной была исходная сингулярность, которая продолжает сохраняться и порождает новые сингулярности в центрах черных дыр (рис. 1.23, в).

Я еще раз обращаю ваше внимание на то, что в стандартных моделях Фридмана существует огромная разница между исходным состоянием и тем состоянием, которое предсказывается теорией для отдаленного будущего. Эта особенность моделей имеет важное значение, поскольку она связана с одним из фундаментальных законов природы — вторым началом термодинамики.

Этот знаменитый закон физики легко объяснить на примерах из обыденной жизни. Каждый из нас может представить или вспомнить простую житейскую ситуацию, когда бокал падает со стола и разбивается, заливая вином ваш любимый коврик (рис. 1.24, последовательность событий слева направо). Проблема заключается в том, что механика Ньютона не содержит никаких запретов на протекание тех же процессов в обратном направлении, хотя никто никогда не видел, чтобы разбитый бокал и пролитое вино соединились снова, заполненный бокал заскочил на стол и т. д. Два разных направления времени указаны на рисунке стрелками, и я вновь повторяю, что по законам механики оба эти направления совершенно равноправны. Разницу между ними устанавливает лишь второе начало термодинамики, в соответствии с которым энтропия системы со временем должна возрастать. Величина, которую я назвал энтропией, значительно возрастает, когда бокал падает и разбивается, вследствие чего процесс и идет в направлении, указанном верхней стрелкой. Грубо говоря, энтропия есть мера беспорядка в системе. Для более глубокого понимания этой идеи нам необходимо ввести представление о так называемом фазовом пространстве.

Рис. 1.24. Законы механики обратимы относительно времени, однако в реальной жизни события всегда протекают в последовательности слева направо (показанной на рисунке), а не наоборот.

Фазовое пространство представляет собой пространство с совершенно немыслимым числом измерений, поскольку каждая его точка описывает координаты и импульсы всех частиц рассматриваемой системы. На рис. 1.25 я выбрал отдельную точку в этом огромном пространстве, и эта точка определяет расположение и характер движения всех частиц системы. При изменении координат и импульсов любой из частиц положение системы в фазовом пространстве изменится. Эволюцию всей системы в таком пространстве я изобразил на рисунке извилистой линией.

Рис. 1.25. Второе начало термодинамики в действии.

С течением времени точка в фазовом пространстве проникает в новые, постоянно увеличивающиеся области (или «отсеки») пространства, в результате чего энтропия системы постоянно увеличивается.

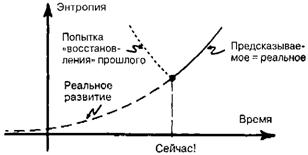
Ломаная линия на рисунке описывает обычную эволюцию системы частиц и не связана ни с каким представлением об энтропии. Для введения энтропии мы должны нарисовать небольшие «пузыри» вокруг областей, в которые последовательно попадает система, и объединить различные состояния, которые нельзя рассмотреть по отдельности. Выражение «нельзя рассмотреть по отдельности» несколько туманно и требует пояснений. Конечно, на самом деле все зависит от того, кто и насколько подробно рассматривает поведение системы. Это один из тех сложных и запутанных вопросов, которые раздражают физиков-теоретиков, когда речь заходит об энтропии. Для нашего рассмотрения будет вполне достаточно указать, что под «невозможностью рассмотреть по отдельности» мы подразумеваем некоторое так называемое «крупнозернистое» объединение группы состояний. Для нахождения энтропии необходимо проделать следующие операции: провести «крупнозернистое» объединение группы состояний (т. е. собрать состояния в некоторой области фазового пространства и «слепить» их в единое целое), определить объем этой области, взять логарифм от объема, а затем умножить его на так называемую постоянную Больцмана. Второе начало термодинамики устанавливает, что энтропия системы постоянно возрастает. Это утверждение может показаться простым и даже глуповатым — фактически постулируется лишь то, что если системе, находящейся в очень маленьком «ящичке» или отсеке, позволить двигаться произвольно, то она будет перебираться во все более крупные «ящики» (что очень похоже на правду хотя бы потому, что большие ящики имеют огромные размеры и у попавшей в них системы практически нет шансов случайно «забрести» в маленький ящик). Вот, пожалуй, и все, что можно сказать по этому поводу, — система, случайным образом блуждающая по фазовому пространству, будет попадать во все более крупные ящики или объемы. Именно это постулируется вторым законом. Впрочем, давайте еще немного подумаем о том, так ли все просто?

На самом деле смысл второго начала значительно шире, и сказанное выше разъясняет его лишь наполовину. Второе начало утверждает, что если нам известно состояние системы сейчас, то мы можем предсказать для нее наиболее вероятные состояния в будущем. Однако этот же закон приводит к совершенно неправильным ответам, как только мы пытаемся придать ему «обратную силу». Действительно, вернемся вновь к примеру с бокалом на краю стола. Разумеется, существует много вариантов, в результате которых бокал может оказаться в данном месте и в данный момент времени. Предположим, что нас интересует, какой из этих вариантов является наиболее вероятным. Применив наши рассуждения в обратном порядке, мы можем придти к выводу, что осколки бокала и пятно на ковре сами собой собрались в целый и наполненный бокал, который затем «подпрыгнул» и очутился на столе. Объяснение очевидно неправильно — гораздо вероятнее, что бокал поставил на край стола кто-то из присутствующих. Но при попытке понять, почему этот кто-то поставил бокал именно здесь, перед нами возникнет целый ряд новых вопросов. Установление причинно-следственных связей в любом случае будет вызывать все новые вопросы, выявлять новые связи и т. д. Только такой путь мог бы привести нас к прошлым состояниям с уменьшающейся энтропией. Правильный ход событий описывается «актуальной» (иначе говоря, «реальной») кривой рис. 1.26 (а не всевозможными попытками восстановления прошлого), т. е. именно той кривой, которой соответствует постоянное уменьшение энтропии по мере перехода к прошлому.

Рис. 1.26.

При попытке объяснения последовательности явлений на рис. 1.24 в обратном порядке мы «навязываем» системе возрастание энтропии при обращении времени, что и приводит к противоречию.

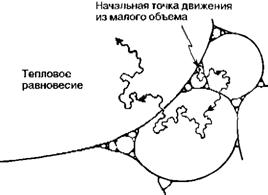
Возрастание энтропии со временем объясняется тем, что система, перемещаясь в фазовом пространстве, занимает все большие объемы-ящики, однако уменьшение энтропии при переходе к прошлому носит совершенно иной характер. Действительно, давайте задумаемся над тем, какие процессы могли бы соответствовать возврату к прошлому с постоянным уменьшением энтропии? Можно ли при этом вернуться к моменту Большого Взрыва? По-видимому, проблема, порождающая столь явные и сильные противоречия, связана с какой-то весьма специфической особенностью самого Большого Взрыва. Попытки объяснения ситуации пока остаются малоуспешными. Например, выше я как-то отметил, что лично не очень доверяю модной теории раздувающейся (инфляционной) Вселенной. В этой достаточно популярной теории наблюдаемая в огромных масштабах однородность Вселенной объясняется событиями, происходившими на самой ранней стадии ее развития. Предполагается, что в момент, когда возраст Вселенной составлял лишь около 10^-36 секунды, произошло какое-то немыслимое по масштабу расширение. Вопрос о том, как выглядела Вселенная на ранней стадии, теряет при этом подходе смысл, поскольку после такого чудовищного мгновенного увеличения объема (приблизительно в 10⁶⁰ раз!) геометрия Вселенной стала выглядеть практически плоской. Это предположение позволяет обойти многие «острые углы», чем, возможно, и объясняются популярность и привлекательность описываемой теории.

Однако, как это часто бывает в теории, предлагаемое объяснение всего лишь заменяет одну очень сложную проблему другой. Дело в том, что для описанного механизма требуется прежде всего, чтобы Вселенная находилась с самого начала в ужасном «беспорядке», который (даже если его чудовищно увеличивать в объеме!) все равно останется «беспорядком», в результате чего по мере расширения ситуация будет становиться все хуже и хуже (рис. 1.27).

Рис. 1.27. Попытка изображения проблемы «внутренне присущей» неупорядоченности Вселенной на ранней стадии развития.

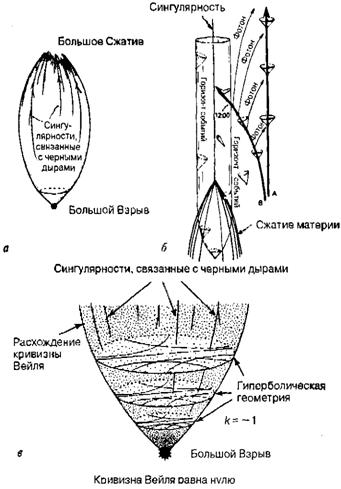
Мне кажется, что приводимые доводы не объясняют наблюдаемую в настоящее время высокую степень упорядоченности Вселенной. Мы нуждаемся в теории, которая могла бы подсказать, на что был похож Большой Взрыв. Очевидно, что будущая теория должна как-то объединить понятия физики макромира и микромира, классической физики и квантовой механики. Более того, будущая теория должна объяснить причины как Большого Взрыва, так и наблюдаемой однородности мира. Возможно, конечно, что теория покончит и со столь понравившейся мне гиперболической вселенной Лобачевского.

Вернемся еще раз к проблеме замкнутости и открытости рассматриваемых вселенных (рис. 1.28) и рассмотрим подробнее процессы формирования черных дыр. Они возникают в результате коллапса материальных объектов, приводящего к образованию сингулярностей, показанных линиями на пространственно-временных диаграммах. Мне хочется предложить вам одну идею, которую я называю гипотезой кривизны Вейля и которая, кстати, не является следствием ни одной из известных теорий. Повторю, что сейчас мы даже не представляем, какой должна быть будущая общая теория, поскольку мы не можем объединить существующие теоретические описания очень больших и очень малых физических объектов. Я уверен, однако, что эта теория должна каким-то образом включить именно то положение, которое я называю гипотезой кривизны Вейля. Напомню, что кривизной Вейля мы называем ту часть тензора Римана, которая связана с искажениями пространства и приливными эффектами. Предлагаемая мною гипотеза состоит в том, что по каким-то пока неясным причинам требуемая комбинация теорий должна приводить к нулевому (или хотя бы к очень малому) значению тензора Вейля в окрестности Большого Взрыва.

Рис. 1.28.

а — общая картина замкнутой вселенной, развитие которой начинается с однородного, низкоэнтропийного Большого Взрыва (с тензором Вейля = 0) и заканчивается высокоэнтропийным Большим Сжатием, соответствующим слиянию многочисленных черных дыр (при этом тензор Вейля стремится к бесконечности); б — пространственно-временная диаграмма, описывающая коллапс отдельной черной дыры; в — эволюция открытой вселенной, также начинающаяся с однородного, низкоэнтропийного Большого Взрыва (с тензором Вейля = 0).

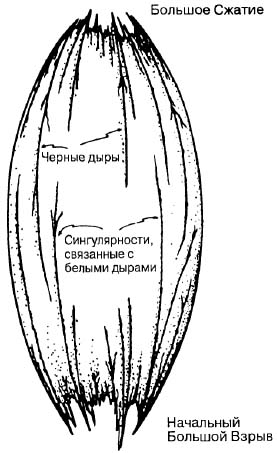
В этом случае общая картина эволюции вселенной будет напоминать рис. 1.28, а и в. Гипотеза кривизны Вейля предполагает асимметрию по отношению ко времени, поэтому она относится лишь к сингулярностям в прошлом, а не в будущем. Если бы тензор Вейля был достаточно «гибким» (т. е. его можно было применять в замкнутой модели и к прошлому, и к будущему), то нам бы удалось покончить с нынешней «ужасающей» картиной мира, в которой вселенная была и остается крайне беспорядочной (рис. 1.29). Ведь Вселенная, в которой мы живем, выглядит совсем по-иному!

Рис. 1.29.

Сняв указанное ограничение (условие, что тензор Вейля = 0), мы вновь получаем картину с высокоэнтропийным Большим Взрывом (тензор Вейля стремится к бесконечности). Такую вселенную пронизывали бы белые дыры, и в ней не выполнялся бы второй закон термодинамики (а это никак не согласуется с тем, что мы видим).

Какова вероятность (строго говоря, случайность или шанс), что начальная сингулярность вселенной была еще слабее, чем нам представляется сейчас? Эту величину можно оценить по формуле Якоба Бекенштейна и Стивена Хокинга для энтропии черных дыр. В нашем случае она приводит к дроби, где в числителе единица, а в знаменателе — немыслимо чудовищное число 10¹⁰ в степени 123. Если указанная формула применима к столь грандиозному объекту, как вселенная, то вы действительно получаете это фантастическое число (поскольку вероятность зависит от размеров). В той вселенной, которую я предлагаю, эту величину можно смело приравнять нулю.

Сказанное подводит нас к вопросу о точности, с которой должны быть определены условия «организации» Большого Взрыва. Ситуация выглядит поразительной, и я попытался выразить ее карикатурой (рис. 1.30), на которой Творец выискивает сверхкрошечную точку в фазовом пространстве, соответствующую начальным условиям, при которых будущая вселенная приобретет привычный нам вид. Творцу необходимо определить положение точки в фазовом пространстве с указанной фантастической точностью (10^{10^123}). Число, о котором идет речь, столь велико, что мне не удалось бы выписать его в ряд, даже используя в качестве нулей все элементарные частицы вселенной.

Рис. 1.30.

Для создания вселенной, похожей на нашу, Творцу пришлось бы найти немыслимо крошечную точку в фазовом пространстве и воткнуть в нее столь же крошечную иголку (ни точку, ни острие иголки на рисунке не удалось изобразить из-за малости размеров!). Выбранная точка должна была содержать лишь 10^{10^123} часть общего объема фазового пространства!

Я начал изложение с проблемы удивительной точности и согласованности физики и математики. Затем я попытался очень кратко рассказать о втором начале термодинамики, которое многие считают «приблизительным» и не оправдавшим возлагавшихся на него надежд (наверное, потому, что оно связано с понятиями случайности и вероятности), но которое на самом деле отражает удивительно точные закономерности. Говоря о вселенной, мы обязаны оценить точность условий создания ее исходного состояния. Эта точность позднее должна быть отражена и в той будущей, еще не созданной теории, которая позволит объединить квантовую теорию и общую теорию относительности. В следующей главе я продолжу рассказ о процессах, объектах и задачах будущей теории.