Глава 9

Философские комментарии к теории истины Тарского^{54}

Главной нашей заботой в науке и в философии является — или должен бы быть — поиск истины на пути смелых догадок и критического поиска того, что ложно в различных наших конкурирующих теориях [292].

Такого взгляда я придерживался тридцать семь лет назад, в июле 1934 года, когда познакомился с Альфредом Тарским на конференции в Праге, организованной «Венским кружком». Я должен, однако, подчеркнуть, что в те дни, до того, как я узнал от Тарского о его теории истины, моя интеллектуальная совесть была далеко не спокойна по поводу допущения, что главной нашей заботой является поиск истины. В моей книге "Logik der Forschung" (1934), гранки которой я привез в Прагу и показал Тарскому (хоть я и не уверен, что они его заинтересовали), я писал: «стремление к знанию и поиск истины остаются сильнейшими стимулами научного открытия»[293]. И все-таки я был неспокоен по поводу понятия истины, и в своей книге я посвятил целый раздел попытке защитить понятие истины как безвредное и соответствующее здравому смыслу, утверждая при этом, что мы, если захотим, можем вообще обойтись без него в методологии науки, говоря взамен о выводимости и тому подобных логических отношениях[294].

Причиной моего беспокойства в связи с понятием истины было, конечно, то, что это понятие в течение некоторого времени подвергалось нападкам ряда философов, причем на весьма серьезных основаниях. Меня пугал не столько парадокс лжеца, сколько трудность объяснения теории истины как соответствия: в чем может состоять соответствие высказывания фактам? К тому же существовал взгляд, который я определенно не разделял, но не чувствовал себя в силах убедительно опровергнуть. Согласно этому взгляду, если мы хотим говорить об истине, мы должны быть способны указать критерий истинности. Я считал, что все равно законно говорить об истине, но я не умел защитить свой взгляд, согласно которому отсутствие критерия истинности не может использоваться как аргумент против логической законности понятия истины.

Я рад, что никогда не выражал в письменном виде это свое беспокойство, которое, как все теперь понимают, было совершенно неоправданным[295]. Сегодня мы знаем, что истина — далеко не единственное понятие, важность и законность которого не отменяются тем фактом, что не существует общего критерия их применимости в отдельных конкретных случаях. Знаменитый пример такого рода — понятие выводимости: мы знаем, что для многих теорий проблема разрешения для теорем неразрешима; и если только мы не ограничим себя лишь разрешимыми теориями, то есть теориями, для которых проблема разрешения решается положительно, то у нас нет никакого критерия или общей процедуры, позволяющей в каждом конкретном случае решить, является ли некоторая предполагаемая теорема данной теории действительно теоремой (valid theorem), то есть выводима ли она с помощью логических средств, предоставляемых этой теорией. (Именно в этом смысле я употребляю термины «верная (valid) теорема», «верный вывод» и т.д.).

Таким образом, в случае неразрешимых теорий у нас нет общего критерия верности или «теоремности (theoremhood)» их формул. Тем не менее, само понятие верности или «теоремности» совершенно ясно даже для неразрешимых теорий: предполагаемая теорема действительно верна (действительно теорема), если и только если существует ее верный вывод, независимо от того, обнаружили мы этот вывод и обнаружим ли его в будущем. Отсутствие критерия ни в какой мере не делает термин «верная теорема» неясным. Всякая неясность в этом случае связана только с тем, что мы не можем обозреть бесконечное множество всех верных выводов, чтобы проверить, не заканчивается ли один из них предполагаемой теоремой. Возможно, нам повезет, и мы обнаружим доказательство или опровержение предполагаемой теоремы; но если нам не повезет, то — если только наша теория не допускает процедуры разрешения — у нас нет никакого способа обнаружить, является ли рассматриваемая формула теоремой или нет.

Сегодня все это почти слишком тривиально для упоминания. Но все еще полно философов, считающих, что любое понятие, например понятие истины, логически законно только в том случае, если существует критерий, позволяющий нам решить, подходит ли некоторый предмет под данное понятие, или нет. Например, в третьем томе «Философской энциклопедии» ("Encyclopedia of Philosophy") 1967 года есть статья[296] в которой мой взгляд, что нет общего критерия истинности научных теорий, резюмируется в виде краткого, но совершенно искажающего этот взгляд положения, в котором мне приписывается мнение, будто «истина сама есть всего лишь иллюзия». А во втором томе этой же энциклопедии нам сообщают, что в поздних работах Витгенштейна предполагается, «что понятие пусто (vacuous), если не существует критерия его применения»[297].

Термин «позитивизм» имеет много значений, но этот (витгенштейнианский) тезис, что «понятие пусто, если не существует критерия его применения», по-моему, выражает самую суть позитивистских тенденций. (Эта идея очень близка к позиции Юма). Если принять эту интерпретацию позитивизма, то позитивизм опровергается современным развитием логики и особенно теорией истины Тарского, которая содержит теорему: для достаточно богатых языков не может быть общего критерия истинности. Эта теорема, конечно, имеет величайший интерес, если вспомнить классический спор между стоиками (а позднее картезианцами) с одной и скептиками с другой стороны. Это один из редких примеров того, как классический философский спор решается, можно сказать, с помощью теоремы, принадлежащей логике или металогике. Но нельзя сказать, что этот пример широко известен среди философов или достойно оценен ими.

Однако я не собираюсь вступать здесь в полемику с философами, отрицающими философское значение теории истины Тарского. Я предпочитаю припомнить глубочайшую радость и облегчение, испытанные мною в 1935 году, когда я осознал, что из теории истины Тарского вытекают следующие выводы:

(1) что это понятие определимо в логических терминах, которые никто еще не ставил под сомнение, и потому логически законно,

(2) что оно применимо к любому недвусмысленно сформулированному (замкнутому) высказыванию (любого не-универсалистского языка), если только оно не применимо к его отрицанию, и потому очевидным образом не пусто, невзирая на то,

(3) что оно не связано ни с каким общим критерием, хотя всякое предложение, выводимое из истинного предложения или из истинной теории, доказуемо (demonstrably) истинно,

(4) что класс истинных предложений образует дедуктивную систему, и

(5) что эта дедуктивная система неразрешима, если только рассматриваемый язык достаточно богат (в связи с этим результатом Тарский ссылается на Гёделя).

Как было упомянуто ранее, я познакомился с Тарским в июле 1934 в Праге. В начале 1935 я снова встретился с ним в Праге на коллоквиуме Карла Менгера, участниками которого были Тарский и Гёдель и на котором я познакомился также с такими великими людьми как Сколем и Абрахам Вальд. Именно тогда я попросил Тарского объяснить мне его теорию истины, что он и сделал в течение двадцатиминутной лекции на скамейке (незабываемая скамейка!) в венском Народном саду (Volksgarten). Он также позволил мне посмотреть гранки немецкого перевода своей великой работы о понятии истины, которые он только что получил от редактора "Studia Philosophica". Никакими словами нельзя описать, как много я из всего этого узнал, и никакими словами нельзя выразить мою благодарность. Хотя Тарский был лишь немногим старше меня и хотя в то время мы были с ним в довольно близком знакомстве, я относился к нему как к единственному человеку, которого по праву мог считать своим учителем в философии. Никогда и ни у кого я столькому не научился, как у него.

Тем не менее есть отдельные второстепенные пункты, по которым я, возможно, расхожусь с ним. Я всегда был философом здравого смысла и реалистом в духе здравого смысла[298]. Моя позиция состояла в том, что здравый смысл (common sense) требует признать, что здравый смысл часто ошибается — быть может, чаще, чем оказывается прав, но ясно, что в философии мы должны исходить из здравого смысла, хотя бы только для того, чтобы обнаружить, путем критики, где он ошибается. Меня интересовал реальный мир, космос, и я решительно противостоял всякого рода идеализму, позитивизму и даже нейтрализму в философии. Если не было бы реального мира, столь же богатого или даже еще более богатого, чем тот, который мы столь поверхностно знаем в нашей повседневной жизни, и если бы исследование этого мира не было главной задачей философии, то философия мне была бы не интересна. Я так и не выяснил точно, как относился Тарский к реализму. Похоже, что на него произвел впечатление «реизм» Котарбинского, но также и венский позитивизм, и он подчеркивал нейтральность своего понятия истины.

Будучи критическим реалистом в духе здравого смысла и сознавая, что тем самым я придерживаюсь «метафизической» теории[299] я не мог не интересоваться тем, что представлялось мне реалистическим аспектом теории истины Тарского — аспектом, само существование которого он, как я подозреваю, мог бы отрицать[300].

Теория Тарского, как вы все знаете и как он первый подчеркивал, является реабилитацией и развитием классической теории, согласно которой истина есть соответствие фактам; и мне кажется, что это значит поддерживать метафизический реализм. В то же самое время теория Тарского есть реабилитация и развитие некоторых моментов классической критики этой теории соответствия, поскольку она показывает, в какой мере были правы те, кто подозревал теорию соответствия в парадоксальности. Последнюю проблему по существу решает учение Тарского о том, что семантика (L₁) некоторого языка-объекта (L₀)— иначе говоря, метаязык, содержащий понятие «истинно в L₀» как определимое понятие — должна быть существенно богаче (более высокого порядка), чем язык-объект (L₀).

Язык-объект Lo, как нам известно, может содержать свой собственный синтаксис и, в частности, дескриптивные имена всех своих выражений. Но L₀ не может, без риска породить антиномии, содержать специфически семантические термины, такие как обозначение (denotation), удовлетворение (satisfaction) или истина, то есть понятия, соотносящие имена выражений L₀ с фактами или объектами, на которые эти выражения ссылаются.

Все это дало мне материал для размышлений, продолжавшихся много лет. Далее я изложу некоторые из этих мыслей.

Если, как предполагает теория Тарского, истина есть соответствие фактам, давайте на время вообще оставим слово «истина» и вместо него будем говорить только о «соответствии высказываний фактам, которые они описывают».

Я думаю, именно кажущаяся невозможность раскрыть или описать это соответствие и делала все теории истины как соответствия до Тарского столь подозрительными — подозрительными даже в глазах людей вроде меня, ценивших теорию соответствия просто за ее реалистический характер, соответствующий здравому смыслу[301].

А теперь проявим смелость и всерьез примем, что есть высказывания, которые соответствуют фактам. Любая теория, имеющая дело с подобной ситуацией, должна иметь возможность говорить: (1) о высказываниях некоторого языка, который мы назовем рассматриваемым языком, или языком-объектом[302]  и (2) о фактах или предполагаемых фактах.

(1) Для того, чтобы говорить о высказываниях, мы должны иметь в своем распоряжении имена для высказываний, например цитирующие имена (quotation names) или описательные (дескриптивные) имена высказываний. Это значит, что любая теория соответствия должна формулироваться на метаязыке, то есть на языке, на котором можно обсуждать или говорить о выражениях некоторого исследуемого языка-объекта.

(2) Чтобы говорить о каких бы то ни было отношениях между высказываниями и фактами, мы должны иметь в своем распоряжении описания фактов; иначе говоря, мы должны быть способны описать на нашем метаязыке все те факты, которые мы можем описать на языке-объекте. Таким образом, метаязык должен содержать переводы высказываний языка-объекта или же должен содержать язык-объект в качестве собственной части (в этом случае мы можем избежать неприятной проблемы существования верных переводов).

Итак, мы установили, что любая теория, имеющая дело с соответствием между высказываниями и фактами и, следовательно, с некоторым отношением между высказываниями и фактами должна формулироваться в метаязыке, имеющем в своем распоряжении, помимо обычных логических слов, еще три вида выражений:

(1) имена высказываний, то есть некоторых языковых выражений языка-объекта; они составляют часть «морфологии» или «синтаксиса» этого языка-объекта;

(2) высказывания, описывающие факты (включая и не-факты), обсуждаемые на этом языке-объекте, то есть переводы с языка-объекта на метаязык (чтобы избежать ловушек перевода, можно сделать язык-объект частью метаязыка, как уже было предложено ранее);

(3) кроме этих двух основных типов выражений есть и третий тип: термины, обозначающие предикаты двух основных типов выражений и отношения между ними, например такие предикаты как «X соответствует фактам» и такие отношения как «X соответствует фактам, если и только если у» (этот последний тип терминов — семантический и имеет более высокий порядок, чем язык-объект, на который они ссылаются).

Таковы три почти очевидные минимальные требования к любому языку, на котором можно было бы сформулировать некоторую теорию соответствия.

Язык, удовлетворяющий этим трем минимальным требованиям, Тарский назвал «семантическим метаязыком».

Я усматриваю величие и смелость достижений Тарского в том, что он открыл эти минимальные требования, а также в том, что он обнаружил, что предикаты и отношения, упомянутые в пункте (3), соотносящие выражения с миром фактов, существенно выходят за пределы средств, которыми мы располагаем в языке-объекте^[303].

Ясно, что, коль скоро мы имеем в своем распоряжении эти три категории выражений, мы можем в семантическом метаязыке делать такие утверждения, как

P соответствует фактам, если и только если p,

принимая при этом, что заглавные курсивные [латинские] буквы, такие как "P", обозначают метаязыковые имена тех высказываний языка-объекта, описывающих факты, метаязыковые переводы которых представлены строчными курсивными буквами, такими как "p".

Преподавая теорию истины Тарского, я обнаружил, что мне и по крайней мере некоторым из моих студентов было легче, когда я употреблял такой способ выражения, то есть говорил не об истине, а о соответствии фактам. Кстати, я обнаружил также, что дело шло легче, если я использовал среди прочих примеров ложные высказывания языка-объекта.

Возьмем в качестве языка-объекта немецкий, а в качестве метаязыка английский^{55}, и вспомним, что переводом немецкого предложения "Der Mond besteht aus grunem Kase" на русский язык будет «Луна состоит из зеленого сыра». Из этих ложных высказываний мы, конечно, можем построить истинное семантическое утверждение:

«Немецкое высказывание "Der Mond besteht aus grunem Kase" истинно, если и только если луна состоит из зеленого сыра».

Использование ложных высказываний языка-объекта, однако, играет лишь незначительную роль. Вместе с тем говорить не об истине, а о соответствии фактам для некоторых студентов может означать серьезную помощь. Это помогает им яснее увидеть (и понять, почему это так, и почему это должно быть так), что высказывание, занимающее место строчной курсивной переменной "p", есть метаязыковое высказывание некоторого факта (или предполагаемого факта), то есть метаязыковое описание некоторого положения дел, описываемого также в языке-объекте.

 Во втором абзаце своей знаменитой статьи об истине[304] Тарский заявляет, что для определения истины ему не нужны никакие семантические понятия (то есть понятия, соотносящие языковые выражения с тем, что они выражают). Однако поскольку он определяет истину с помощью понятия удовлетворения (satisfaction), а это последнее понятие, очевидно, семантическое (на что указывает сам Тарский в первом абзаце своей работы "The Establishment of Scientific Semantics" на p. 401 в "Logic, Semantics, Metamathematics"), внимательного читателя можно извинить, если он поначалу почувствует некоторое недоумение. Рассеять это недоумение можно следующим образом. Каждый достаточно богатый язык, на котором говорится о некоторой предметной области, может (согласно результатам, полученным независимо друг от друга Тарским и Гёделем) содержать свои собственные «морфологию» или «синтаксис», в то время как (что показал Тарский) никакой непротиворечивый язык не может содержать средств определения своей собственной семантики. Для определения истины Тарскому нужен, как мы видим, семантический метаязык более высокого порядка, чем язык-объект, семантику которого этот метаязык содержит. Заметим, однако, что термины, являющиеся семантическими по отношению к языку-объекту, в метаязыке могут иметь тот же статус, что и другие морфологические или синтаксические термины. Таким образом, семантика языка-объекта L_n может быть частью синтаксиса метаязыка более высокого порядка (скажем, L_n+1): в L_n+1 могут не входить никакие термины неморфологического или несинтаксического характера. Это равносильно сведению семантики языка L_n к синтаксису языка L_n+1.

Этот момент имеет общефилософский интерес не только потому, что на семантические термины принято было смотреть с подозрением, но и потому, что всякое сведение подозрительных терминов к общепринятым терминам заслуживает нашего внимания. Во всяком случае, достижение Тарского, сумевшего свести термины, принадлежащие семантике языка L_n, к несемантическим терминам языка L_n+1, устраняет всякие основания для подозрительности.

Я считаю это сведение важным, поскольку в философии мы не часто имеем возможность ввести совершенно новую (и притом подозрительную) категорию терминов на основе (свободных от всяческих подозрений) установленных категорий. Это — реабилитация, акт спасения чести подозреваемого термина.

Вместе с тем я рассматриваю определения и вопросы сводимости как философски не особенно важные. Если мы не можем определить термин, ничто не мешает нам использовать его как неопределяемый: использование неопределяемых терминов не только законно, но и неизбежно, поскольку всякий определяемый термин должен в конечном счете определяться через некоторые неопределяемые термины[305]. По моему мнению, работу Тарского делает столь философски важной не описание им успешного способа определения «истинности», а реабилитация им теории истины как соответствия и доказательство того, что нас не ждут никакие дальнейшие трудности, коль скоро мы поняли существенную потребность в семантическом метаязыке, более богатом, чем язык-объект и его синтаксис. Достаточно ясно, что мы, если захотим, можем начать с примитивных семантических терминов (как это делает Р. М. Мартин [306]), вместо того, чтобы старательно их избегать. И мы получим по существу ту же самую семантическую теорию истины как соответствия фактам, но без теории Тарского, которая показывает возможность построения семантического метаязыка, свободного от любых специфически семантических терминов, нам, скорее всего, не удалось бы преодолеть подозрительности философов по отношению к семантическим терминам.

Как было упомянуто ранее, я реалист. Я признаю, что такой идеализм, как кантовский, можно защищать в той мере, в какой он утверждает, что все наши теории созданы человеком и что мы пытаемся наложить их на мир природы. Но я реалист постольку, поскольку считаю, что ответ на вопрос о том, истинны или нет созданные человеком теории, зависит от реальных фактов — реальных фактов, которые, за очень немногими исключениями, явным образом не созданы человеком. Наши созданные человеком теории могут приходить в столкновение с этими реальными фактами, и тогда в наших поисках истины нам приходится приспосабливать теории к фактам или же отказываться от этих теорий.

Теория Тарского позволяет нам определить истину как соответствие фактам, но мы можем также использовать ее для того, чтобы определить реальность (действительность) как то, что соответствует истинным суждениям. Например, мы можем отличить реальные факты, то есть (предполагаемые) факты, которые реальны, от (предполагаемых) фактов, которые нереальны (то есть от не-фактов). Или более явно: мы можем сказать, что предполагаемый факт — например то, что луна состоит из зеленого сыра — является реальным фактом, если и только если описывающее его высказывание (такое, как «Луна состоит из зеленого сыра») истинно; в противном случае предполагаемый факт не является реальным фактом (или, если вы предпочитаете говорить так, вообще не является фактом).

И точно так, как Тарский позволил нам заменить термин «истина» на «множество истинных высказываний (или предложений)», мы можем заменить термин «реальность» на «множество реальных фактов».

Таким образом, я предполагаю, что если мы можем определить понятие истины, мы может определить и понятие реальности. (Конечно, при этом возникает проблема порядка, аналогичная проблеме порядка языков в работе Тарского, см. особенно его «Постскриптум» на р. 268-277 "Logic, Semantics, Metamathematics"). Я не собираюсь этим сказать, что термин «истина» в каком-либо смысле более фундаментален, чем термин «реальность»: я хотел бы отвергнуть любое подобное предположение из-за его идеалистического привкуса[307]. Я просто хочу сказать, что если возможно определить «истину» как «соответствие фактам» или, что сводится к тому же, как «соответствие реальности», то в равной мере возможно определить «реальность» как «соответствие истине». А поскольку я реалист, мне хотелось бы иметь возможность быть спокойным на тот счет, что понятие реальности не «пусто» и ни по какой — той или иной причине — не является подозрительным; во всяком случае оно не более подозрительно, чем понятие истины.

Среди более ранних теорий Тарского, доступных для неискушенного философа, такого как я, есть его теория исчисления систем. Я был в Париже в 1935 году, когда, если мне не изменяет память, Тарский закончил свою работу об исчислении систем ("Calculus of System") [308]. Она меня очень заинтересовала.

Я попытался скомбинировать некоторые из наиболее очевидных результатов работы Тарского об истине с результатами его работы по исчислению систем. Мы сразу же получаем следующие в высшей степени тривиальные теоремы, в которых предполагается, что упоминаемые в них языки не универсалистские (universalistic).

Теорема. Множество T истинных высказываний любого языка есть дедуктивная система в смысле исчисления систем Тарского. Эта система полна [309].

Как дедуктивная система, T представляет собой класс (всех собственных) следствий (consequence class); это значит, что он совпадает с классом Cn(T) своих собственных логических следствий (T=Cn(T)).Эта система полна в том смысле, что если к T прибавить любое высказывание, не принадлежащее T, получившийся класс будет противоречивым.

Теорема. Множество истинных высказываний любого достаточно богатого языка есть неаксиоматизируемая дедуктивная система в смысле исчисления систем Тарского.

Обе эти теоремы совершенно тривиальны и в дальнейшем изложении будет предполагаться, что рассматриваемые языки достаточно богаты, чтобы удовлетворять второй из них.

Теперь я введу новое понятие — понятие истинностного содержания высказывания a.

Определение. Множество всех истинных высказываний, следующих из любого данного высказывания a, называется истинностным содержанием a.Это — дедуктивная система.

Теорема. Истинностное содержание любого истинного высказывания A есть аксиоматизируемая система A_T= А; истинностное содержание любого ложного высказывания a есть дедуктивная система A_T?А, где A_T неаксиоматизируема, если только рассматриваемый язык-объект достаточно богат.

Это определение и эту теорему можно обобщить. Исчисление дедуктивных систем Тарского можно рассматривать как обобщение исчисления высказываний, поскольку каждому высказыванию (или классу логически эквивалентных высказываний) a соответствует (финитно) аксиоматизируемая система A,такая что

А=Cn(А)=Cn({а})

и наоборот: каждой аксиоматизируемой дедуктивной системе A соответствует некоторое высказывание (или класс логически эквивалентных высказываний) a. Поскольку же существуют также неаксиоматизируемые дедуктивные системы или классы следствий, такие что не существует высказываний или конечных классов высказываний, классом следствий которых они бы являлись, переход от высказываний к классам следствий или дедуктивным системам или от исчисления высказываний к исчислению систем можно назвать обобщением.

Таким образом, мы имеем — в более общем виде — для каждого класса следствий или дедуктивной системы A систему A_T — истинностное содержание A. Она совпадает с A, если и только если A состоит только из истинных высказываний, и в любом случае она есть подсистема A: очевидно, A_T есть произведение, или пересечение, множеств А и T.

Можно задать вопрос: соответствует ли истинностному содержанию А_Т высказывания a или дедуктивной системы A также нечто, что можно было бы назвать ложностным содержанием А_F высказывания а или дедуктивной системы A? Кажется естественным определить ложностное содержание дедуктивной системы A как класс всех ложных высказываний, принадлежащих A, но это будет не вполне удовлетворительно, если мы хотим использовать (как я предлагаю) термин «содержание» как третий синоним к терминам «дедуктивная система» и «класс следствий». Ведь этот класс, состоящий, по предположению, только из ложных высказываний, не является дедуктивной системой: всякая дедуктивная система A содержит истинные высказывания — собственно говоря, бесконечное число истинных высказываний, — так что класс, состоящий исключительно из ложных высказываний, принадлежащих A, не может быть содержанием.

Чтобы ввести понятие ложностного содержания А_F высказывания a или класса следствий A, можно обратиться к понятию относительного содержания A при данном B, которое можно ввести как обобщение дедуктивной системы в смысле Тарского, или (абсолютного) содержания A=Cn(A).Я попытаюсь разъяснить это понятие, и ввиду возможной интуитивной критики я введу также понятие меры содержания. В конце этой главы я введу с помощью понятия мер истинностного содержания и ложностного содержания понятие степени приближения к истине, или правдоподобности (verisimilitude).

Тарский говорит о больших или меньших дедуктивных системах или классах следствий. Действительно, множество дедуктивных систем (для некоторого языка) частично упорядочено отношением включения, совпадающим с отношением выводимости. Следующее замечание, высказанное Тарским в его работе об исчислении систем, можно использовать как ключ к релятивизации классов следствий, или содержаний, или дедуктивных систем: «среди дедуктивных систем существует наименьшая, то есть являющаяся подсистемой всех других дедуктивных систем. Это система Cn(0)— множество следствий пустого множества. Эта система, которая здесь для краткости будет обозначаться L, может интерпретироваться как множество всех логически верных (valid) предложений (или, в более общем виде, как множество всех тех предложений, которые мы признаем за истинные с самого начала, когда принимаемся строить дедуктивную теорию, являющуюся предметом... нашего исследования)» [310].

Это наводит на мысль, что мы можем использовать вместо нулевой системы L какую-то другую систему «в качестве множества всех тех предложений, которые мы признаем за истинные с самого начала, когда принимаемся строить, и т.д.». Обозначим, как и ранее, дедуктивную систему, содержанием которой мы интересуемся, переменной "A", а «множество всех тех предложений, которые мы признаем за истинные с самого начала», переменной "B". Тогда мы можем написать выражение

Cn(А,В)

как релятивизацию (relativization) Cn(А) Тарского, которое является особым случаем при В= L = Cn(0):

Cn(А)=Cn(A,L).

Мы можем писать сокращенно "A,B" вместо "Cn(A,B)", точно так же, как Тарский пишет "A" вместо "Cn(A)".Процитированный отрывок из Тарского подсказывает следующее определение:

Определение: А,В=Cn(А,В) = Cn (A+B) - Cn(B).

А отсюда очевидным образом следует

Теорема:

A=Cn(A)=A,L=Cn(А,L)=Cn(A+L)-Cn(L).

Ограничиваясь относительным способом записи, мы получаем для истинностного содержания

А_Т=AT,L=Cn((А.Т)+L)- Cn(L),

а для ложностного содержания

A_F = A, A_T= Cn(A+ A_T) - Cn(A_T) = Cn(A) - Сп(А_T),

что превращает ложностное содержание в относительное содержание, объем (extension) которого совпадает (как первоначально и предлагалось) с классом всех ложных высказываний в А.

 Против предложенного определения ложностного содержания Ар как относительного содержания А₎Ат можно выдвинуть следующее возражение. Это определение интуитивно опирается на цитату из Тарского, в которой Тарский принимает L за наименьшую или нулевую дедуктивную систему. Вместе с тем в нашей последней теореме

А=A,L=Cn(А+L)-Cn(L)

мы воспринимали слово «нулевая» слишком буквально: теперь мы видим, что L следует понимать как множество меры нуль, а не как множество, которое, с учетом нашего выражения "-Cn(L)", в буквальном смысле пусто или которого больше нет, согласно нашему определению, поскольку оно было вычтено (так что в A остались только нелогические высказывания, чего мы не имели в виду).

Относимся мы к этому возражению серьезно или нет, оно в любом случае исчезает, если мы решим оперировать с мерой содержания ct(A) или ct(A,B),а не с самим содержанием, или классом следствий Cn(А) или Cn(А,В).

В 1934 году Тарский привлек внимание пражской конференции к аксиоматизации исчисления относительной вероятности дедуктивной системы А при данной дедуктивной системе В, предложенной Стефаном Мазуркевичем[311] и опирающейся на исчисление систем Тарского. Такую аксиоматизацию можно рассматривать как введение функции меры для дедуктивных систем или содержаний А, В, С,... , даже хотя данная конкретная функция — функция вероятности

р(А,В)

и возрастает с уменьшением относительного содержания. Это наводит на мысль ввести меру содержания с помощью определения, такого как

Определение: ct(A, В) = 1 - p(А, В).

Эта функция возрастает и убывает с возрастанием и убыванием относительного содержания. (Возможны, конечно, и другие определения, но это кажется самым простым и очевидным). Мы сразу же получаем:

ct(L) = 0

ct(A_T) = 1 - p(А.T, L) = 1 - р(А.Т)

ct(A_F) = 1- p(A,A_T),

что соответствует ранее полученным результатам.

Это наводит на мысль, что мы можем ввести понятие правдоподобности, или verisimilitude, высказывания а таким образом, чтобы оно возрастало вместе с возрастанием истинностного содержания этого высказывания и убывало с ростом его ложностного содержания. Это можно сделать несколькими способами [312].

Самый очевидный способ — принять ct(A_t) - ct(A_F) за меру правдоподобности A. Однако по причинам, которые я здесь не буду обсуждать, мне кажется несколько более предпочтительным определить правдоподобность vs(A) как разность, умноженную на некий нормализующий множитель, предпочтительно следующий: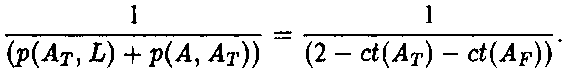

Таким путем мы получаем следующее

Определение: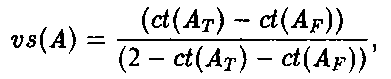

что, конечно, можно переписать в р-нотации как: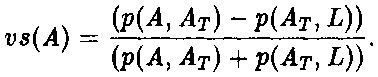

А это приводит к

-1 ? vs(A) ? +1

 и, в частности, к

vs(L) =  0.

Иначе говоря, правдоподобность измеряет не ту степень приближения к истине, которой можно достичь, не делая никаких содержательных высказываний (она измеряется нехваткой содержания или вероятностью), а приближение ко «всей истине» — через все большее и большее истинностное содержание. Я полагаю, что правдоподобность в этом смысле является более адекватной целью науки — особенно естественных наук, чем истина, по двум причинам. Во-первых, потому, что мы не думаем, что L составляет цель науки, даже хотя L=L_T. Во-вторых, потому, что мы можем предпочесть теории, которые считаем ложными, другим, даже истинным — таким как L, — если сочтем, что их истинности содержание существенно превышает их ложностное содержание.

В этих заключительных разделах главы 9 я лишь кратко очертил программу сочетания теории истины Тарского с его исчислением систем с целью получить понятие правдоподобности, позволяющее нам говорить — без опасения говорить бессмыслицу — о теориях, являющие лучшими или худшими приближениями к истине. Я, конечно, не предполагаю, что может существовать критерий применимости этого понятия не более, чем может существовать такой критерий для понятия истины. Вместе с тем некоторым из нас (например, Эйнштейну) иногда хочет говорить такие вещи, как например что у нас есть основания предполагать, что эйнштейновская теория тяготения не истинна, но являет лучшим приближением к истине, чем ньютоновская. Иметь возможное со спокойной совестью говорить подобные вещи кажется мне важным пожеланием к методологии естественных наук.

Добавление

Замечание к определению истины по Тарскому^{56}

 В своей знаменитой работе о понятии истины[313] Тарский описывает способ определения понятия истины или, точнее, понятия «x есть истинное высказывание (языка L)».Первоначально этот способ применялся к исчислению классов, но он может применяться в самом общем виде к самым разным (формализованным) языкам, включая языки, позволяющие формализовать некоторые эмпирические теории. Для этого способа характерно то, что определение «истинного высказывания» основывается на определении отношения удовлетворения (relation of satisfaction), или точнее — выражения «бесконечная последовательность f удовлетворяет пропозициональной функции Х»[314]. Это отношение удовлетворения интересно само по себе, вне зависимости от того, что оно играет решающую роль в определении истины (и что шаг от определения удовлетворения к определению истины практически не представляет трудности). Предлагаемые мною замечания связаны с проблемой применения при определении удовлетворения конечных, а не бесконечных последовательностей. Это, по-моему, желательно с точки зрения применения данной теории к эмпирическим наукам, а также и с дидактической точки зрения.

Сам Тарский кратко обсуждает два способа [315] связанные с применением конечных последовательностей переменной длины вместо бесконечных последовательностей, но он указывает и на некоторые недостатки этих альтернативных способов. Первый из них ведет к «значительным [или „довольно серьезным"] осложнениям» (ziemlich bedeutenden Komplikationen) при определении удовлетворения (Определение 22), в то время как недостаток второго состоит в «некоторой искусственности» (eine gewisse Kunstlichkeit), поскольку он приводит к определению истины (Определение 23 [р. 195 англ. перевода]) с помощью понятия «пустой последовательности», или «последовательности нулевой длины»[316]. В своих замечаниях я хочу обратить внимание на то, что сравнительно небольшое изменение процедуры Тарского позволяет нам оперировать с конечными последовательностями, не сталкиваясь с осложнениями или искусственностями (например, пустыми последовательностями), которые имел в виду Тарский. Этот способ позволяет нам сохранить весьма естественную процедуру, предусмотренную условием (6)Определения 22 Тарского (р. 193 англ. перевода), и таким образом избежать обходного пути, связанного с введением отношений — или свойств, — имеющих порядок, равный числу свободных переменных рассматриваемой пропозициональной функции. Предлагаемое мною изменение способа Тарского достаточно незначительно, но ввиду того, что Тарский ссылается на другие его варианты, имеющие значительные недостатки, а не на данный вариант, может быть, стоит описать и это небольшое улучшение[317].

Для этой цели полезно будет неформально упомянуть, во-первых понятие номера места n (place number n) (или n-го места) в конечной последовательности объектов, а во-вторых, понятия длины конечной последовательности f, то есть число мест в f (символически Np(f))равное самому большому номеру места в ней, и сравнения конечны последовательностей по их длине. Упомянем, в-третьих, что объект может занимать в последовательности определенное место — скажем, n-е, -и тогда его можно назвать [n-м индивидом или] n-м объектом, или n-м членом рассматриваемой последовательности. Следует отметить, что один и тот же объект может занимать разные места в одной последовательности так же как и в разных последовательностях[318].

Как и Тарский, я использую символы "f₁", "f₂", ... , "f_i", "f_k"» ... "f_n" в качестве имен объектов, занимающих первое, второе, i-е, k-e, ... n-е места в последовательности f. Я пользуюсь обозначениями Тарского за тем исключением, что [по типографским соображениям] использув "P_ky" для обозначения обобщения [или квантификации по общности выражения y по переменной v_k[319]. Принимается, что к Определению (11)[320] Тарского добавлено Определение выражения «v_k входит в пропозициональную функцию x» — это предположение ни в коей мере не выводит нас за пределы методов Тарского и фактически в неявном виде присутствует в процедурах самого Тарского.

Теперь мы можем заменить Определение 22 Тарского [р. 193]. Мы заменим его двумя определениями — предварительным Определением 22a и Определением 22b, которое соответствует собственному определению Тарского.

Определение 22а. Конечная последовательность объектов f адекватна пропозициональной функции x(или достаточно длинна относительно x), если и только если

для каждого натурального числа n,

если v_n входит в x, то число мест в f по крайней мере равно n (то есть Np(f) ? n).

Определение 22b [321].

Последовательность f удовлетворяет пропозициональной функции x, если и только если

f — конечная последовательность объектов,

x — пропозициональная функция, и

(1) f адекватна x,

(2) x соблюдает одно из следующих четырех условий:

(?) Существуют натуральные числа i и k такие, что x= l_i,k и f_i ? f_k.

(?) Существует пропозициональная функция y такая, что x = y, и f не удовлетворяет y.

(?) Существуют две пропозициональные функции у и z такие, что x = y + z и f удовлетворяет либо y, либо z, либо обеим.

(?) Существует натуральное число k и пропозициональная функция y такая, что

(a) x = P_ky,

 (b) любая конечная последовательность g, длина которой равна f, удовлетворяет y, если только g соблюдает следующее условие: для любого натурального числа n, если n — номер места в f и n?k, то g_n = f_n.

Теперь Определение 23 Тарского [р. 193] можно заменить любым из двух следующих эквивалентных[322] определений:

Определение 23+. x — истинное высказывание (то есть x?Wr), если и только если (а) x — высказывание (x?As) и (b) любая конечная последовательность объектов, адекватная x, удовлетворяет x.

Определение 23++. x — истинное высказывание (то есть x?Wr), если и только если (a) x — высказывание (x?As) и (b) существует по крайней мере одна конечная последовательность объектов, удовлетворяющая х.

Можно заметить, что Определение 23++ не требует предположения об адекватности упоминаемой последовательности. Можно также заметить, что в Определении 23+ (которое в точности соответствует определению Тарского) — но не в 23++ — условие (а) можно заменить условием «x — пропозициональная функция», достигая тем самым определенного обобщения, в частности, на пропозициональные функции со свободными переменными, такими как, например, функция l_i,i, то есть на универсально-значимые (allgemeingultige [верные для любой индивидуальной предметной области]) пропозициональные функции[323].

Аналогичным образом определение 23++, если распространить его на функции, приводит к понятию удовлетворимой (erfullbare) пропозициональной функции.

В заключение скажу, что в применении к эмпирической теории (по крайней мере частично формализованной) и особенно к неквантифицированным пропозициональным функциям такой теории, определение выполнения [или удовлетворения], то есть Определение 22Ь, выглядит совершенно «естественным» с интуитивной точки зрения, в основном потому, что оно обходится без бесконечных последовательностей [324].

Примечания:

2

Popper K. R. Ein Kriterium des empirisches Charakters theoretischer Systeme // Erkenntnis, Bd. 3, 1933. S.426 и далее (русский перевод: Поппер К. Критерий эмпирического характератеоретических систем / Поппер К. Логика и рост научного знания. Избранные работы. Общая редакция Садовского В. И. М.: Прогресс, 1983. С. 236-239).

3

Popper К. Я. Logik der Forschung. Julius Springer Verlag, Vienna, 1934 (в дальнейшем при ссылках эта работа будет обозначаться как L. d. F.). См. также Popper К. Я. The Logic of Scientific Discovery. Hutchinson. London, 1959 (в дальнейшем обозначается как L. Sc. D.).

29

Jennings H.S. The Behaviour of the Lower Organisms. Columbia University, 1906.

30

Cm. Hume D. Treatise..., p. 265.

31

Казалось бы, об этом можно и не говорить, но в американской «Философской энциклопедии» мне приписывают следующее мнение: «Истина сама по себе не более, чем иллюзия» (Encyclopedia of Philosophy. 1967. Vol.2. P. 37).

32

Berkeley G. Three Dialogues Between Hylas and Philonous, диалог второй: «Для меня будет достаточным основанием не верить... если я не вижу оснований верить». Что касается Юма, то см. C.&R., р. 21 (где цитируется его работа "Enquiry Concerning Human Understanding", Section V, Part I (русский перевод см. Юм Д. Исследование о человеческом разумении. М.: Прогресс, 1995. С. 62)).

292

Эта формулировка главной нашей заботы в науке несколько улучшена — применительно к естественным наукам — в последнем разделе этой главы. Здесь можно сказать кое-что о терминологии.

Мне кажется неинтересной (поскольку она в основном вербальная) проблема того, должны мы говорить о «предложениях» (sentences), «высказываниях» (statements) или «пропозициях» (propositions). Те, кто критикует Тарского за употребление термина «предложение», утверждают в основном, что предложения суть неинтерпретированные цепочки слов, соблюдающие некоторые правила грамматики, и как таковые не могут быть ни истинными, ни ложными. Они упускают из вида тот факт, что Тарский явным образом говорит об «осмысленных (meaningful) предложениях» и только об интерпретированных языках. Чтобы показать свое презрение к подобного рода вербальной критике, я просто принял терминологию моих оппонентов и во всей этой работе говорю не о «предложениях», а о «высказываниях». Таким образом, я использую «высказывание» как синоним интерпретированного, осмысленного предложения, или пропозиции.

293

Popper К. R. The Logic of Scientific Discovery, section 85, p. 278.

294

Popper К. R. Op. cit., section 84.

295

См. особенно примечание 1 на p. 254 в Tarski A. Logic, Semantics, Metamathematics. Oxford, Clarendon Press, 1956.

296

См. The Encyclopedia of Philosophy. Ed. by Edwards Paul, Macmillan, 1967. Vol. 3. P. 37.

297

Ibidem. Vol. 2. P. 260. Ср. мое «Открытое общество» (русский перевод: Лоппер К. Р. Открытое общество и его враги. Тт. 1-2. М., 1992), т. 2, Добавление 1, раздел 3.

298

Я реалист в двух смыслах этого слова. Во-первых, я верю в реальность физического мира. Во-вторых, я верю в реальность мира теоретических объектов, как я объяснил это в моих работах «Эпистемология без субъекта знания», «О теории объективного разума» и «Реалистический взгляд на логику, физику и историю» (теперь это главы 3, 4 и 8 настоящей книги. В них я сохраняю свою оппозицию эссенциализму — признанию реальности понятий, но утверждаю реальность проблем, теорий, ошибок и т. п.

(Что касается первого смысла, я могу даже назвать себя материалистом постольку, поскольку я верю в реальность материи, хотя я самым решительным образом не материалист, если понимать «материализм» как взгляд, согласно которому (протяженная) материя есть нечто окончательное и ни к чему не сводимое или что только она реальна. Напротив, я верю, что может существовать истинная теория материи, объясняющая протяженность материи интенсивностями, такими как силы, что впервые было предположено Лейбницем, Бошковичем и Кантом).

299

Ср. мою книгу "The Logic of Scientific Discovery", p. 251-252, текст к прим. *1 (В этом примечании дается отсылка к Приложению *1Х к "The Logic of Scientific Discovery" и к разделу *29 книги Поппера «Реализм и цель науки» (Popper К. Realism and the Aim of Science. London and N.Y., Routledge, 1995), составляющей первый том трехтомного «Постскриптума к „Логике научного исследования"» — Прим. пер.).

300

Ср. Tarski A. The Semantic Conception of Truth and the Foundations of Semantics // Philosophy and Phenomenological Research. 1944. Vol.4. Pp.341-376; см. особенно раздел 19.

301

Подробнее см. Popper К. R. Conjectures and Refutations, а также главы 2 и 8 настоящей книги.

302

Похоже, что термин "object language" (буквально — «объектный язык») первоначально был введен для обозначения «языка, на котором говорят о (физических) объектах». Я использую его в смысле «язык, являющийся объектом исследования»: он исследуется теорией, формулируемой на метаязыке. (Это, конечно наводит на мысль о бесконечной иерархии метаязыков).

303

Лишь немногим менее философски важный результат относительно терминов типа (3) состоит в том, что как термины метаязыка они имеют тот же морфологический характер, что и термины типа (I); иначе говоря, они принадлежат морфологии, построенной в метаязыке (хотя и не той ее части, которая содержит морфологию и синтаксис языка-объекта и может быть построена в самом языке-объекте).

304

Ср. с. 152 английского перевода этой статьи Вуджера в книге: TarskiA. Logic, Semantics, Metamathematics, Oxford, Clarendon Press, 1956. (См. также прим. 13 на с. 340. — Прим. ред.)

305

Так, Тарский подчеркивал, что понятие истины можно было бы ввести не через определение, а через аксиомы.

306

См. Martin R.M. Truth and Denotation. A Study in Semantical Theory. London, Routledge & Keagan Paul, 1958.

307

См. Popper K.R. Conjectures and Refutations, примечание 33 на p. 116 с выражением признательности Александру Койрё.

308

См. Тарский A, Logic, Semantics, Metamathematics. Oxford, Clarendon Press, 1956, pp. 342-383.

309

Я в основном следую символике Тарского (особенно в том, что касается употребления заглавных курсивных букв для обозначения дедуктивных систем), за исключением того, что для класса истинных высказываний, который Тарский обозначает Tr, я использую символ T.

310

Tarski A. Logic, Semantics, Metamathematics. Oxford, Clarendon Press, p, 343.

311

Тарский ссылается на работу: Mazurkiewicz S. Die Grundlagen der Wahrscheiningskeits-rechnung I. Monatshefte tur Mathematik & Physik, Band 41, 1934, SS. 343-352. Из сноски 2 на S. 344 этой работы видно, что исчисление систем Тарского было известно польским математикам еше в 1930 году. Система Мазуркевича имеет определенный финитистский характер в отличие от моей собственной системы (см. Popper К. R. The Logic of Scientific Discovery, pp. 326-358), которую можно интерпретировать различными способами, например как исчисление вероятностей дедуктивных систем.

Я могу, пожалуй, упомянуть, что в настоящей работе я использую в качестве символов для функций меры, таких как вероятность, содержание и правдоподобность, строчные курсивные буквы, например, р(А), ct(A), vs(A). (Добавлено в 1978 г.) Везде, где это необходимо, я принимаю «тонкую структуру» вероятности. См. Popper К. R.  Logic of Scientific Discovery, New Appendix *VIL

312

См. Popper К. R. Conjectures and Refutations, Addendum 3, pp. 391-397.

313

См. Tarski А. Der WahrheitsbegrifT in den formalisierten Sprachen // Studia Philosophica, Bd. I, 1935, S. 261 [англ. пер.: Tarski A. The Concept of Truth in Formalized Languages// TarskiA. Logic, Semantic, Metamathematics, 1956, paper VIII, pp. 152-278]. Как я понимаю, Тарский предпочитает переводить «Aussage» и «Aussagefunktion» как «sentence» («предложение») и «sentence-function» («сентенциальная функция») — термины, используемые в переводе логических работ Тарского на английский, выполненным профессором Вуджером, — тогда как я пользуюсь здесь терминами «высказывание (statement)» и «пропозициональная функция (statement function)». Перевод Вуджера должен быть вскоре опубликован издательством Clarendon Press в Оксфорде. [Эта книга вышла в 1956 году. Есть и еще несколько различий между моим переводом и переводом Вуджера].

314

См. Tarski Л. Ibidem, S. 311 [p. 193], S. 313 [p. 195]. Заметим, что класс пропозициональных функций (или сентенциальных функций) включает класс высказываний, то есть замкнутых пропозициональных функций.

315

Первый из этих альтернативных способов очерчен Тарским в примечании 40 на S. 309 и далее [р. 191 англ. перевода, прим. 1]. (Там не говорится явно, что этот способ можно использовать для избежания бесконечных последовательностей, но ясно, что его можно для этого использовать). Второй метод описывается в примечании 43 на S. 313 и далее [р. 195 англ. перевода, прим. 1]. Способ, предложенный Тарским в этом примечании, технически слегка отличный от примененного Тарским в основном тексте, используется Карнапом в его «Введении в семантику» (Сатар R. Introduction to Semantics, 1942, pp.47 и далее [точнее pp. 45-48]). Хотя Карнап ссылается на Тарского, он упускает из вида то, что Тарский предвидел этот конкретный способ. (В прим. 7 на S.368 [р. 245 англ. перевода, прим. 2] Тарский указывает еще и третий способ — очень простой, но безусловно в высшей степени искусственный в понимании Тарского; более того, этот способ относится только к определению истины как таковому, а не к определению выполнения [удовлетворения], которое интересно само по себе).

316

 Карнап также использует это искусственное понятие.

317

 Основное различие между моим способом и способами, предлагаемыми Тарским (упомянутыми ранее в прим. 3) состоит в следующем. Тарский предлагает ставить в соответствие данной функции (либо бесконечные последовательности, либо) конечные последовательности определенной (зависящей от данной функции) длины, в то время как я использую конечные последовательности «достаточной длины» (Определение 22а), то есть не слишком короткие для рассматриваемой функции. Соответственно, мои конечные последовательности могут быть любой длины (свыше определенного минимума, зависящего от рассматриваемой функции). Но допущение конечных функций любой длины (если этого достаточно для наших целей) не приводит ни к какой неоднозначности, поскольку мы легко получаем теорему (ср. Лемму А.Тарского на S. 317 [р. 198 англ. перевода]), согласно которой, если f удовлетворяет x, то всякое g, являющееся расширением f, также удовлетворяет x (где g есть расширение f, если и только если для каждого f_i существует g_i такое, что g_i = f_i). Таким образом, эта теорема говорит, что нам достаточно рассматривать только самые короткие конечные последовательности из тех, которые адекватны рассматриваемой функции (конечно, всей рассматриваемой сложной функции, в отличие от ее компонентов).

318

Объекты (things) [так я называю их здесь; я мог бы называть их, как Тарский «индивидами», если бы не то, быть может, слегка запутывающее обстоятельство, что «индивиды» Тарского представляют собой индивидуальные классы исчисления классов] рассматриваемые Тарским в этом разделе его работы, суть классы; учитывая сказанное Тарским в параграфах 4 и 5, я буду говорить здесь о «последовательностях объектов» а не о последовательностях классов, имея в виду, что для любых объектов f_i и f_k, определено отношение вхождения f_i ? f_k.

319

Ср. Определение 6 Тарского на S. 292 [р. 176 англ. перевода].

320

Tarski A. Ibidem, S. 294 [р. 178 англ. перевода]. Тарский явным образом определяет только выражение «переменная входит свободно в пропозициональную функцию x» [или Vf есть свободная переменная поопозипиональной функции

321

Это в точности напоминает Определение 22 Тарского [р. 193], за исключением того, что к условию Тарского добавлен пункт (1) (чтобы заменить бесконечные последовательности конечными), и что наш пункт (6) содержит небольшое изменение, поскольку в нем говорится о длине f (и д). [Перевод "erfullen" как «удовлетворять» имеет тот недостаток, что в определении выражения «f удовлетворяет x» используется интуитивное представление о том, что «x соблюдает (то есть удовлетворяет) такие-то условия». Но эти два «удовлетворяет» технически совершенно различны, хотя интуитивно и очень близки. В немецком тексте на S. 311 не проводится никакого терминологического различия, но на S. 312 в сноске, соответствующей сноске 1 на р. 193 английского издания, имеет место различие  между «erfьllt» и «befriedigt». В Определении 22, конечно, нет никакого круга].

322

Их эквивалентность следует из соображений Тарского; ср. Ibidem, S. 313, строки с 13 по 16 [р. 194, строки с 12 по 15 англ. перевода].

323

Ср. Ibidem, S. 320 [р. 201], Определение 27 и последующие.

324

 Мы можем использовать его, например, чтобы определить случай выполнения некоторого закона (записанного не как обобщение, то есть записанного без квантора общности впереди) как конечную последовательность объектов, удовлетворяющих этому закону, или — что мне кажется более важным — чтобы определить опровергающий пример для любой (открытой или замкнутой) пропозициональной функции как конечную [и адекватную] последовательность объектов, не удовлетворяющую ей.